
【题目】如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.

【答案】∠C与∠AED相等
【解析】试题分析:∠C与∠AED相等.由邻补角定义得到∠1与∠DFE互补,再由已知∠1与∠2互补,根据同角的补角相等可得出∠2与∠DFE相等,根据内错角相等,两直线平行,得到AB与EF平行,再根据两直线平行,内错角相等可得出∠3与∠ADE相等,由已知∠B与∠3相等,利用等量代换可得出∠B与∠ADE相等,根据同位角相等,两直线平行,得到DE与BC平行,再根据两直线平行,同位角相等可得证.
试题解析:解:∠C与∠AED相等.理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义),
∴∠2=∠DFE(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∠B=∠3(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠C=∠AED(两直线平行,同位角相等).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )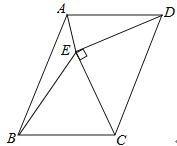
A.120°
B.135°
C.150°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
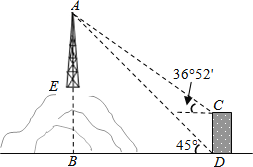
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=![]() ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为________(结果保留π)
,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为________(结果保留π)
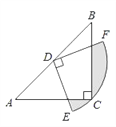
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌冰箱启动后开始降温,如果冰箱启动时的温度是10℃,每小时冰箱内部的温度降低5℃(降至设定温度后即停止降温),那么3小时后冰箱内部温度是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外学习小组有5人,在一次数学测验中的成绩分别是120、130、135、120、125,下列说法不正确的是( )
A.众数是120
B.方差是34
C.中位数是135
D.平均数是126
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形三个内角的度数分别是(x+y)°,(x-y)°,x°,且x>y>0,则该三角形有一个内角为( )
A. 30°
B. 45°
C. 90°
D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前,组委会拟定了四种记分方案:方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
打分 | 7.0 | 7.8 | 3.2 | 8.0 | 8.4 | 8.4 | 9.8 | 8.0 | 8.4 | 8.0 |
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com