【题目】某校举行“做文明郴州人”演讲比赛，聘请了10位评委为参赛选手打分，赛前，组委会拟定了四种记分方案：方案一：取所有评委所给的平均分；
方案二：在所有评委给的分中，去掉一个最高分，去掉一个最低分，取剩余得分的平均分；
方案三：取所有评委给分的中位数；
方案四：取所有评委给分的众数．
为了探究四种记分方案的合理性，先让一名表演选手（不参加正式比赛的）演讲，让10位评委给演讲者评分，表演者得分如下表：
评委编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
打分 | 7.0 | 7.8 | 3.2 | 8.0 | 8.4 | 8.4 | 9.8 | 8.0 | 8.4 | 8.0 |
（1）请分别用上述四种方案计算表演者的得分；
（2）如果你是评委会成员，你会建议采用哪种可行的记分方案？你觉得哪几种方案不合适？
【答案】【解答】解：（1）方案一最后得分：
（7.0+7.8+3.2+3×8+3×8.4+9.8）=7.7；
方案二最后得分：
（7.0+7.8+3×8+3×8.4）=8；
方案三最后得分：8；
方案四最后得分：8和8.4．
（2）因为方案1中的平均数受极端数值的影响，不适合作为这个同学演讲的最后得分，
所以方案1不适合作为最后得分的方案；
【解析】（1）根据给出的方案和平均数的计算公式分别进行解答即可；
（2）考虑不受极值的影响，不能有两个得分等原因进行排除，即可得出答案．
【考点精析】本题主要考查了算术平均数和中位数、众数的相关知识点，需要掌握总数量÷总份数=平均数．解题关键是根据已知条件确定总数量以及与它相对应的总份数；中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数
过（﹣2，4），（﹣4，4）两点．
（1）求二次函数
的解析式；
（2）将沿x轴翻折，再向右平移2个单位，得到抛物线
，直线y=m（m＞0）交于M、N两点，求线段MN的长度（用含m的代数式表示）；
（3）在（2）的条件下，、交于A、B两点，如果直线y=m与、的图象形成的封闭曲线交于C、D两点（C在左侧），直线y=﹣m与、的图象形成的封闭曲线交于E、F两点（E在左侧），求证：四边形CEFD是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．
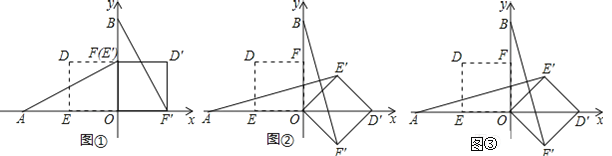
（1）如图②，当α=135°时，求AE′，BF′的长；
（2）如图③，当0°﹤α﹤180°时， AE′和BF′有什么位置关系；
（3）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程（x-3）(x-2)-p2=0.
（1）求证：无论p取何值时，方程总有两个不相等的实数根；
（2）设方程两实数根分别为x1、x2，且满足x12+x22=3 x1x2，求实数p的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
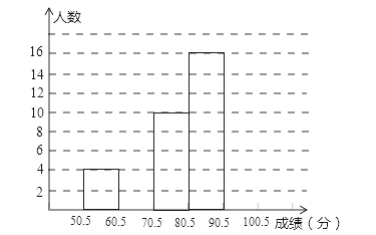
【题目】为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有850名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）进行统计．请你根据尚未完成并有局部污染的频率分布表和频率分布直方图，解答下列问题：
分 组 | 频数 | 频率 |
50.5～60.5 | 4 | 0.08 |
60.5～70.5 | 0.16 | |
70.5～80.5 | 10 | |
80.5～90.5 | 16 | 0.32 |
90.5～100.5 | ||
合 计 | 50 | 1.00 |
（1）填充频率分布表的空格；
（2）补全频数直方图，并在此图上直接绘制频数分布折线图；
（3）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？
（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
