
【题目】如图,已知二次函数![]() 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.

(1)求二次函数![]() 的解析式;
的解析式;
(2)将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,直线y=m(m>0)交
,直线y=m(m>0)交![]() 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,![]() 、
、![]() 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与![]() 、
、![]() 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与![]() 、
、![]() 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)根据待定系数法即可解决问题.
(2)先求出抛物线y2的顶点坐标,再求出其解析式,利用方程组以及根与系数关系即可求出MN.
(3)用类似(2)的方法,分别求出CD、EF即可解决问题.
试题解析:(1)∵二次函数![]() 过(﹣2,4),(﹣4,4)两点,∴
过(﹣2,4),(﹣4,4)两点,∴![]() ,解得:
,解得: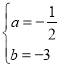 ,∴二次函数
,∴二次函数![]() 的解析式
的解析式![]() .
.
(2)∵![]() =
=![]() ,∴顶点坐标(﹣3,
,∴顶点坐标(﹣3,![]() ),∵将
),∵将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,∴抛物线
,∴抛物线![]() 的顶点坐标(﹣1,
的顶点坐标(﹣1,![]() ),∴抛物线
),∴抛物线![]() 为
为![]() ,由
,由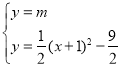 ,消去y整理得到
,消去y整理得到![]() ,设
,设![]() ,
,![]() 是它的两个根,则MN=
是它的两个根,则MN=![]() =
=![]() =
=![]() ;
;
(3)由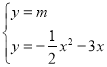 ,消去y整理得到
,消去y整理得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则CD=
,则CD=![]() =
=![]() =
=![]() ,由
,由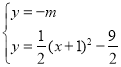 ,消去y得到
,消去y得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则EF=
,则EF=![]() =
=![]() =
=![]() ,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.
,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.
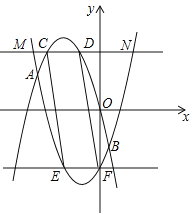


科目:初中数学 来源: 题型:
【题目】若代数式(4x2-mx-3y+4)-(8nx2-x+2y-3)的值与字母x的取值无关,求代数式(-m2+2mn-n2)-2(mn-3m2)+3(2n2-mn)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数a,b在数轴上对应的A,B两点之间距离![]() .
.
探究运用
①数轴上表示1和3两点之间的距离是_____;数轴上表示x和2两点之间的距离是_____.
②根据图像比较大小: ![]() ______
______![]() (填“<”、“=”、“>”).
(填“<”、“=”、“>”).
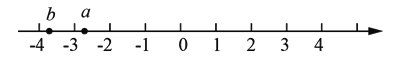
拓展延伸
③若点A.B、C在数轴上分别表示数-1、4、c,且点C到点A.B的距离之和是7,则c=_____.
④关于x的方程![]() (m>n,k>0),借助数轴探究方程的解的情况,直接写出结论.
(m>n,k>0),借助数轴探究方程的解的情况,直接写出结论.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
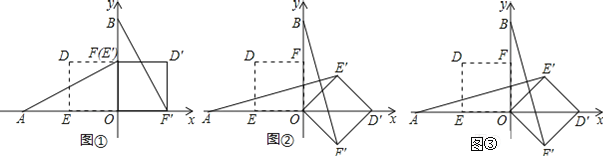
(1)如图②,当α=135°时,求AE′,BF′的长;
(2)如图③,当0°﹤α﹤180°时, AE′和BF′有什么位置关系;
(3)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课余生活,某校举行联欢晚会,在联欢晚会上,有A,B,C三名同学站在一个三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放在△ABC的( )
A. 三边中线的交点处 B. 三条角平分线的交点处 C. 三边高的交点处 D. 三边垂直平分线的交点处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com