
����Ŀ����a��b�������϶�Ӧ��A��B����֮�����![]() ��
��
̽������
�������ϱ�ʾ1��3����֮��ľ�����_____�������ϱ�ʾx��2����֮��ľ�����_____��
�ڸ���ͼ��Ƚϴ�С�� ![]() ______
______![]() �����������=��������������
�����������=��������������
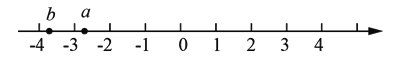
��չ����
������A��B��C�������Ϸֱ��ʾ��-1��4��c���ҵ�C����A��B�ľ���֮����7����c=_____��
�ܹ���x�ķ���![]() ��m��n��k��0������������̽�����̵Ľ�������ֱ��д��������
��m��n��k��0������������̽�����̵Ľ�������ֱ��д��������
![]()
���𰸡���1��4�� ![]() ����2��������3��-2��5����4���𰸼�������
����2��������3��-2��5����4���𰸼�������
�����������������
��1���ɡ���������A��B�����Ӧ����Ϊa��b����A��B����֮�����![]() �����м��㼴�ɵõ�����𰸣�
�����м��㼴�ɵõ�����𰸣�
��2����![]() ���
���![]() ��ʾ�������ϱ�ʾ��-3���ĵ㵽��ʾ����
��ʾ�������ϱ�ʾ��-3���ĵ㵽��ʾ����![]() ���ĵ�֮��ľ���ɵñ�����ۣ�
���ĵ�֮��ľ���ɵñ�����ۣ�
��3���֣���![]() ����
����![]() ����
����![]() ������������ۼ��ɵõ�����𰸣�
������������ۼ��ɵõ�����𰸣�
��4���֣���![]() ����
����![]() ����
����![]() ������������ۼ��ɵõ������.
������������ۼ��ɵõ������.
���������
��1�������� ��
�������ϱ�ʾ1��-3�������ľ���Ϊ�� ![]() ��
��
�������ϱ�ʾ![]() ��-2�������ľ���Ϊ��
��-2�������ľ���Ϊ�� ![]() ��
��
��2����![]() ����
����![]() ��ʾ�������ϱ�ʾ��-3���ĵ㵽��ʾ����
��ʾ�������ϱ�ʾ��-3���ĵ㵽��ʾ����![]() ���ĵ�֮��ľ�����
���ĵ�֮��ľ����� ![]() ��ʾ�������ϱ�ʾ��-3���ĵ㵽��ʾ����
��ʾ�������ϱ�ʾ��-3���ĵ㵽��ʾ����![]() ���ĵ�֮��ľ��룬
���ĵ�֮��ľ��룬
����ͼ�ɵ��� ![]() ��
��
��3���������֪����C����A��B����ľ���֮��Ϊ�� ![]() ��
��
����![]() ʱ��
ʱ�� ![]() �ɻ�Ϊ��
�ɻ�Ϊ�� ![]() ����ã�
����ã� ![]() ��
��
����![]() ʱ��
ʱ�� ![]() �ɻ�Ϊ��
�ɻ�Ϊ�� ![]() ����ʱ�ֳ��⣻
����ʱ�ֳ��⣻
����![]() ʱ��
ʱ�� ![]() �ɻ�Ϊ��
�ɻ�Ϊ�� ![]() ����ã�
����ã� ![]() ��
��
��4������![]() ʱ��������
ʱ��������![]() �ɻ�Ϊ��
�ɻ�Ϊ�� ![]() ����ã�
����ã� ![]() ��
��
����![]() ʱ��������
ʱ��������![]() �ɻ�Ϊ��
�ɻ�Ϊ�� ![]() ����ʱ�����⣻
����ʱ�����⣻
����![]() ʱ��������
ʱ��������![]() �ɻ�Ϊ��
�ɻ�Ϊ�� ![]() ����ã�
����ã� ![]() .
.
��������������x�ķ���![]() ��m��n��k��0���Ľ�Ϊ��
��m��n��k��0���Ľ�Ϊ�� ![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ı߳�Ϊa�������Խ���AC��BD�ཻ�ڵ�O��P������AB������һ�㣬��P��ֱ���ֱ��AC��BD�Ĵ���PE��PF������ΪE��F��
��1����ͼ1����P�����߶�AB��ʱ��PE+PF��ֵ�Ƿ�Ϊ��ֵ������ǣ����������ֵ��������ǣ������˵����
��2����ͼ2����P�����߶�AB���ӳ�����ʱ����PE��PF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������4��4��4��5��5��6��7����������λ���ֱ��ǣ� ��
A.4��4B.4��5C.7��5D.7��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������A1B1C1D1 ��D1E1E2B2 ��A2B2C2D2 ��D2E3E4B3 ��A3B3C3D3 ��������ͼ��ʾ�ķ�ʽ���ã����е�B1��y���ϣ���C1��E1��E2��C2��E3��E4��C3������x���ϣ���֪������A1B1C1D1 �ı߳�Ϊ1����B1C1O=60�㣬B1C1��B2C2��B3C3������������A2017B2017C2017D2017�ı߳���_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���![]() ������2��4��������4��4�����㣮
������2��4��������4��4�����㣮

��1������κ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ��x�ᷭ�ۣ�������ƽ��2����λ���õ�������
��x�ᷭ�ۣ�������ƽ��2����λ���õ�������![]() ��ֱ��y=m��m��0����
��ֱ��y=m��m��0����![]() ��M��N���㣬���߶�MN�ij��ȣ��ú�m�Ĵ���ʽ��ʾ����
��M��N���㣬���߶�MN�ij��ȣ��ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2���������£�![]() ��
��![]() ����A��B���㣬���ֱ��y=m��
����A��B���㣬���ֱ��y=m��![]() ��
��![]() ��ͼ���γɵķ�����߽���C��D���㣨C����ࣩ��ֱ��y=��m��
��ͼ���γɵķ�����߽���C��D���㣨C����ࣩ��ֱ��y=��m��![]() ��
��![]() ��ͼ���γɵķ�����߽���E��F���㣨E����ࣩ����֤���ı���CEFD��ƽ���ı��Σ�
��ͼ���γɵķ�����߽���E��F���㣨E����ࣩ����֤���ı���CEFD��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ij���д�һ¥����¥��һ�Զ����ݣ�ͼ2�Dz���ʾ��ͼ����֪�Զ�����AB���¶�Ϊ1��2��4��AB�ij�����13�ף�MN�Ƕ�¥¥����MN��PQ��C��MN�ϴ����Զ����ݶ���B�����Ϸ���һ�㣬BC��MN�����Զ����ݵ�A�����C�������Ϊ42�������¥�IJ��BCԼΪ�����ף��� sin42���0��7��tan42���0��9��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��ij�е�������ֵԼΪ2041��Ԫ����2041��Ԫ�ÿ�ѧ��������ʾΪ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com