练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于x的方程m2x2+（4m﹣1）x+4=0的两个实数根互为倒数，那么m的值为（　　）
    A.2
    B.-2
    C.±2
    D.±

    【答案】B
    【解析】解：∵方程m2x2+（4m﹣1）x+4=0的两个实数根互为倒数，
    ∴=1，解得m=2或m=﹣2，
    当m=2时，方程变形为4x2+7x+4=0，△=49﹣4×4×4＜0，方程没有实数解，
    所以m的值为﹣2．
    故选B．
    【考点精析】通过灵活运用一元二次方程的定义和求根公式，掌握只有一个未知数，并且未知数的项的最高系数为2的方程为一元二次方程；根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某课外学习小组有5人，在一次数学测验中的成绩分别是120、130、135、120、125，下列说法不正确的是（　　）
    A.众数是120
    B.方差是34
    C.中位数是135
    D.平均数是126

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我市开展的“‘新华杯’中学双语课外阅读”活动中，某中学为了解八年级400名学生读书情况，随机调查了八年级50名学生读书的册数．统计数据如下表所示：

    册数

    0

    1

    2

    3

    4

    人数

    2

    10

    15

    17

    6

    （1）求这50个样本数据的众数和中位数；
    （2）根据样本数据，估计该校八年级400名学生在本次活动中读书多于2册的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校举行“做文明郴州人”演讲比赛，聘请了10位评委为参赛选手打分，赛前，组委会拟定了四种记分方案：方案一：取所有评委所给的平均分；
    方案二：在所有评委给的分中，去掉一个最高分，去掉一个最低分，取剩余得分的平均分；
    方案三：取所有评委给分的中位数；
    方案四：取所有评委给分的众数．
    为了探究四种记分方案的合理性，先让一名表演选手（不参加正式比赛的）演讲，让10位评委给演讲者评分，表演者得分如下表：

    评委编号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    打分

    7.0

    7.8

    3.2

    8.0

    8.4

    8.4

    9.8

    8.0

    8.4

    8.0

    （1）请分别用上述四种方案计算表演者的得分；
    （2）如果你是评委会成员，你会建议采用哪种可行的记分方案？你觉得哪几种方案不合适？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班为了从甲、乙两同学中选出班长，进行了一次演讲答辩和民主测评，A、B、C、D、E五位老师作为评委，对“演讲答辩”情况进行了评价，全班50位同学参与了民主测评，结果如下表：
    表一 演讲答辩得分

    表二 民主测评得票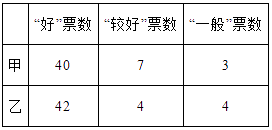

    规则：①演讲答辩得分按“去掉一个最高分和一个最低分后，再算出平均分”的方法确定；②民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分；③演讲答辩得分和民主测评得分按4：6确定权重，计算综合得分，请你计算一下甲、乙的综合得分，选出班长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年00：12：14，天猫双十一总成交额超36200000000元，已超过2013年双十一全天的成交额，其中36200000000用科学记数法表示为：_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

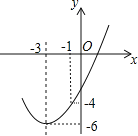
    【题目】如图，已知顶点为(-3，-6)的抛物线经过点(-1，-4)，则下列结论中错误的是（ ）

    A. B.

    C. 若点(-2，)，(-5，) 在抛物线上，则 D. 关于的一元二次方程的两根为-5和-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】韦达定理：若一元二次方程ax2+bx+c=0（a≠0）的两根分别为x1、x2 ， 则x1+x2=﹣ ， x1x2= ， 阅读下面应用韦达定理的过程：
    若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 ， 求x12+x22的值．
    解：该一元二次方程的△=b2﹣4ac=42﹣4×（﹣2）×1=24＞0
    由韦达定理可得，x1+x2=﹣=﹣=2，x1x2===﹣
    x12+x22=（x1+x2）2﹣2x1x2
    =22﹣2×（﹣）
    =5
    然后解答下列问题：
    （1）设一元二次方程2x2+3x﹣1=0的两根分别为x1 ， x2 ， 不解方程，求x12+x22的值；
    （2）若关于x的一元二次方程（k﹣1）x2+（k2﹣1）x+（k﹣1）2=0的两根分别为α，β，且α2+β2=4，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将抛物线y＝3x2的图象先向下平移3个单位，再向左平移4个单位所得的解析式为（　　）

    A.y＝3（x﹣3）2+4B.y＝3（x+4）2﹣3

    C.y＝3（x﹣4）2+3D.y＝3（x﹣4）2﹣3

    查看答案和解析>>

    同步练习册答案