
【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣![]() , x1x2=
, x1x2=![]() , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣![]() =﹣
=﹣![]() =2,x1x2=
=2,x1x2=![]() =
=![]() =﹣
=﹣![]()
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣![]() )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1 , x2 , 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
【答案】解:(1)∵一元二次方程的△=b2﹣4ac=32﹣4×2×(﹣1)=17>0,
由根与系数的关系得:x1+x2=﹣![]() , x1x2=﹣
, x1x2=﹣![]() ,
,
∴![]() +x22=(x1+x2)2﹣2x1x2=
+x22=(x1+x2)2﹣2x1x2=![]() =
=![]() ;
;
(2)由根与系数的关系知:![]() =﹣k﹣1,αβ=
=﹣k﹣1,αβ=![]() =k﹣1,
=k﹣1,
α2+β2=((α+β)2﹣2αβ=(k+1)2﹣2(k﹣1)=k2+3
∴k2+3=4,
∴k=±1,
∵k﹣1≠0
∴k≠1,
∴k=﹣1,
将k=﹣1代入原方程:﹣2x2+4=0,
△=32>0,
∴k=﹣1成立,
∴k的值为﹣1.
【解析】(1)先根据根与系数的关系得到x1+x2=﹣![]() , x1x2=﹣
, x1x2=﹣![]() , 再利用完全平方公式变形得到x12+x22=(x1+x2)2﹣2x1x2 , 然后利用整体代入的方法计算即可;
, 再利用完全平方公式变形得到x12+x22=(x1+x2)2﹣2x1x2 , 然后利用整体代入的方法计算即可;
(2)根据一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,求出两根之积和两根之和的关于k的表达式,再将α2+β2=4变形,将表达式代入变形后的等式,解方程即可.
【考点精析】掌握根与系数的关系是解答本题的根本,需要知道一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
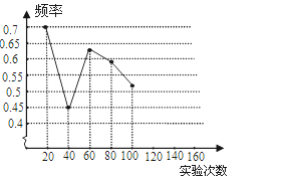
【题目】一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 |
| 78 | 88 |
相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 |
|
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
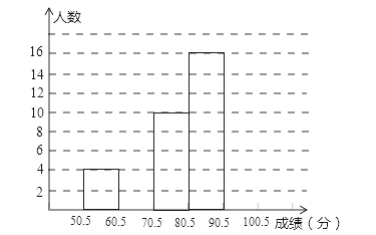
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:
分 组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合 计 | 50 | 1.00 |
(1)填充频率分布表的空格;
(2)补全频数直方图,并在此图上直接绘制频数分布折线图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】sin65°与cos26°之间的关系为( )
A.sin65°<cos26°B.sin65°>cos26°
C.sin65°=cos26°D.sin65°+cos26°=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com