[题目]a.b为有理数.现在规定一种新的运算“⊕ .如a⊕b＝﹣ab+a2﹣1.则(2⊕3)⊕(﹣3)＝．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】a、b为有理数，现在规定一种新的运算“⊕”，如a⊕b＝﹣ab+a2﹣1，则（2⊕3）⊕（﹣3）＝_____．

【答案】﹣1

【解析】

直接利用新定义将原式变形,计算即可得出答案．

解：∵a⊕b＝﹣ab+a2﹣1，

∴（2⊕3）⊕（﹣3）

＝（﹣2×3+4﹣1）⊕（﹣3）

＝﹣3⊕（﹣3）

＝3×（﹣3）+（﹣3）2﹣1

＝﹣1．

故答案为：﹣1．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在我市开展的“‘新华杯’中学双语课外阅读”活动中，某中学为了解八年级400名学生读书情况，随机调查了八年级50名学生读书的册数．统计数据如下表所示：

册数	0	1	2	3	4
人数	2	10	15	17	6

（1）求这50个样本数据的众数和中位数；
（2）根据样本数据，估计该校八年级400名学生在本次活动中读书多于2册的人数．

查看答案和解析>>

科目：初中数学 来源： 题型：

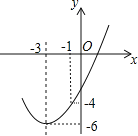
【题目】如图，已知顶点为(-3，-6)的抛物线经过点(-1，-4)，则下列结论中错误的是（）

A. B.

C. 若点(-2，)，(-5，) 在抛物线上，则 D. 关于的一元二次方程的两根为-5和-1

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】韦达定理：若一元二次方程ax2+bx+c=0（a≠0）的两根分别为x1、x2 ，则x1+x2=﹣ ， x1x2= ，阅读下面应用韦达定理的过程：
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 ，求x12+x22的值．
解：该一元二次方程的△=b2﹣4ac=42﹣4×（﹣2）×1=24＞0
由韦达定理可得，x1+x2=﹣=﹣=2，x1x2===﹣
x12+x22=（x1+x2）2﹣2x1x2
=22﹣2×（﹣）
=5
然后解答下列问题：
（1）设一元二次方程2x2+3x﹣1=0的两根分别为x1 ， x2 ，不解方程，求x12+x22的值；
（2）若关于x的一元二次方程（k﹣1）x2+（k2﹣1）x+（k﹣1）2=0的两根分别为α，β，且α2+β2=4，求k的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

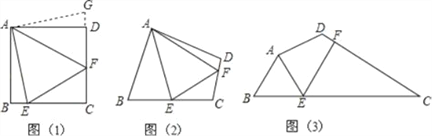
【题目】问题：如图(1)，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．

【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图（1）证明上述结论．

【类比引申】如图(2)，四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时，仍有EF=BE+FD．

【探究应用】如图(3)，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据： =1.41， =1.73）