Question

【题目】如图，在中， 是它的角平分线， 是上的一点， ， 分别平分， ， ，垂足为点．

求证：（ ）．（）．

Answer 1

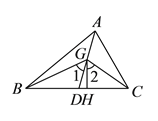
【答案】见解析．

【解析】试题分析：（1）由三角形内角和定理可知∠ABC+∠ACB=180°﹣∠BAC，然后利用角平分线的性质即可求出∠BGC=90°+∠BAC．

（2）由AD是角平分线，得到∠BAD=∠CAD，然后根据图形可知：∠1=∠BAD+∠ABG，∠2=90°﹣∠GCH，最后根据三角形的内角和定理以及外角的性质即可求出答案．

试题解析：解：（1）由三角形内角和定理可知：∠ABC+∠ACB=180°﹣∠BAC．∵BG，CG分别平分∠ABC，∠ACB，∠GBC=∠ABC，∠GCB=∠ACB，∴∠GBC+∠GCB=（∠ABC+∠ACB）=（180°﹣∠BAC）=90°﹣∠BAC，∴∠BGC=180°﹣（∠GBC+∠GCB）=180°﹣（∠ABC+∠ACB）=90°+∠BAC；

（2）∵AD是它的角平分线，∴∠BAD=∠CAD，∴∠1=∠BAD+∠ABG．∵GH⊥BC，∴∠GHC=90°，∴∠2=90°﹣∠GCH=90°﹣∠ACB=90°﹣（180°﹣∠DAC﹣∠ADC）

=∠DAC+∠ADC．

∵∠ADC=∠ABC+∠BAD，∴ ∠ADC=∠ABC+∠∠BAD=∠ABG+∠BAD，∴∠2=∠DAC+∠ADC=∠BAD+∠BAD+∠ABG=∠BAD+∠ABG，∴∠1=∠2．