
����Ŀ����ͼ����Rt��ACB�У���C=90�㣬AC=30cm��BC=25cm������P�ӵ�C��������CA�����˶����ٶ���2cm/s������Q�ӵ�B��������BC�����˶����ٶ���1cm/s��
��1�������P��Q�������25cm��
��2���������PCQ����ABC������
��3������CPQ�����ΪS1����ABC�����ΪS2�����˶��������Ƿ����ijһʱ��t��ʹ��S1��S2=2��5�������ڣ����t��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��10���P��Q�������25cm����2��![]() ���
���![]() �����PCQ����ABC��������3���˶�10���15��ʱ��S1��S2=2��5
�����PCQ����ABC��������3���˶�10���15��ʱ��S1��S2=2��5
�������������������1����x���P��Q�������25cm����x��ʾ��CP��CQ�����ݹ��ɶ����г����̣��ⷽ�̼��ɣ���2������PCQ�ס�ACB����PCQ�ס�BCA����������������������ε������г���ϵʽ���ⷽ�̼��ɣ���3����t�ֱ��ʾ��CP��CQ�����������г����̣��ⷽ�̼��ɣ�
�����������1����x���P��Q�������25cm��
��CP=2xcm��CQ=��25��x��cm��
��������2x��2+��25��x��2=252 ��
��ã�x1=10��x2=0����ȥ����
��10���P��Q�������25cm
��2����y���ɽ��PCQ����ABC���ƣ�
����PCQ����ACBʱ�� ![]() =
=![]() ����
���� ![]() ��
��
��ã�y=![]() ��
��
����PCQ����BCAʱ�� ![]() =
= ![]() ����
����![]() ��
��
��ã�y= ![]() ��
��
��![]() ���
���![]() �����PCQ����ABC����
�����PCQ����ABC����
��3����CPQ�����ΪS1=![]() ��CQ��CP=
��CQ��CP=![]() ��2t����25��t��=��t2+25t��
��2t����25��t��=��t2+25t��
��ABC�����ΪS2= ![]() ��AC��BC=375��
��AC��BC=375��
������ã�5����t2+25t��=375��2��
��ã�t1=10��t2=15��
���˶�10���15��ʱ��S1��S2=2��5



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ���ҵġ�һ��һ·�����÷�չս�ԣ�����Ʒ����ʶ�������ʼ첿�Ŷ�A��B��C��D�ĸ�����������ͬ���ͺŵ������2000�����кϸ��ʼ�⣬ͨ�����ó�C���ҵĺϸ���Ϊ95%�������ݼ�����ݻ�������ͼ1��ͼ2������������ͳ��ͼ��
��1�����D���ҵ����Ϊ�� ����������ͳ��ͼ��D���Ҷ�Ӧ��Բ�Ľ�Ϊ�� ����
��2�����C���ҵĺϸ����Ϊ�� ����������ͼ1����������
��3��ͨ������˵���ϸ�������ǰ�����������������ң�
��4����Ҫ��A��B��C��D�ĸ������У������ȡ�������Ҳμӵ¹���ҵ��Ʒ�����ᣬ���á��б�����������ͼ���ķ��������3������������ͬʱ��ѡ�еĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ조��������ˮϵ��̬�������̡����ȣ���ˮ��������������10̨��ˮ�����豸������A��B�����ͺŵ��豸��ÿ̨�ļ۸�ֱ�Ϊa��Ԫ��b��Ԫ��ÿ�´�����ˮ���ֱ�Ϊ240�֣�200�֣���֪����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
��1����a��b��ֵ��
��2������Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ���ļ��ֹ�����
��3���ڣ�2���������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ��ˮ���������һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��뾶Ϊ1��Բ��ԭ�������x�����������һ�ܣ�Բ��һ����ԭ��O�����O�䣬Բ��Ҳ�ӵ�A�����A�䣮
��1����O��������� ����A��������� ��
��2������P��Բ�ڹ���������Բ�ľ�����ijһλ�ã����Ե�P����O����O��Ϊ����������ε������
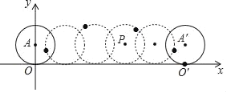
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����ۺ�ʵ����У�ͬѧ������������ֱ��������Ӳֽ�壬һ�麬��30��ǣ�һ�麬��45��ǣ�������һ��ֱ�DZ�����ȵģ��ֽ���45��ǵ�ֱ��������Ӳֽ���ص����ں�30��ǵ�ֱ��������Ӳֽ���ϣ������ǵ�ֱ����ȫ�غϣ���ͼ2������ȵ�ֱ�DZ�AC��Ϊ12cm������һ��ֱ�DZ�û���ص�����BD�ij�������ø��ű�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �еĵ�
�еĵ�![]() ������
������![]() ������Ϊ
������Ϊ![]() ���� ��
���� ��![]() ������ ��
Ϊ������ ��![]() ����Ƶ�
����Ƶ�![]() Ϊ��
Ϊ��![]() �ġ�
�ġ�![]() �������㡱 �� ���磺
�������㡱 �� ���磺![]() �ġ� 2 �������㡱Ϊ
�ġ� 2 �������㡱Ϊ![]() ����
����![]() ��
��
���� ��![]() �ġ� 3 �������㡱
�ġ� 3 �������㡱 ![]() ������Ϊ������
������������
���� ����![]() �ġ� 5 �������㡱
�ġ� 5 �������㡱 ![]() ������Ϊ
������Ϊ![]() �����
�����![]() �����ꣻ
�����ꣻ
���� ����![]() ��
��![]() ����������ϣ� ��
����������ϣ� ��![]() �ġ�
�ġ�![]() �������㡱Ϊ
�������㡱Ϊ![]() �㣬 ���߶�
�㣬 ���߶�![]() �ij���Ϊ�߶�
�ij���Ϊ�߶�![]() ���ȵ� 2 ���� ��
���ȵ� 2 ���� ��![]() ��ֵ ��
��ֵ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������8��ͬ����С����������ɵ�ħ�������Ϊ8.

��1��������ħ�����ⳤ��
��2��ͼ������Ӱ������һ��������![]() �������Ӱ���ֵ��������߳�.
�������Ӱ���ֵ��������߳�.
��3����������![]() �ŵ������ϣ���ͼ�ڣ�ʹ�õ�
�ŵ������ϣ���ͼ�ڣ�ʹ�õ�![]() ��
��![]() �غϣ���ô��
�غϣ���ô��![]() �������ϱ�ʾ����Ϊ________.
�������ϱ�ʾ����Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�Ƿ���������![]() ͼ���ϵ�һ�㣬����A��AB��
ͼ���ϵ�һ�㣬����A��AB��![]() ���ڵ�B������AOB�����Ϊ2����A������Ϊ
���ڵ�B������AOB�����Ϊ2����A������Ϊ![]() ��
��

��1����m��k��ֵ��
��2����һ�κ���y=ax+3��ͼ����A����˫���ߵ���һ֧�ڵ�C����y���ڵ�D������AOC�������
��3����![]() �����Ƿ���ڵ�P��ʹ����PAC�����Ϊ6��������ڣ��������P�����ꣻ�������ڣ���˵��������
�����Ƿ���ڵ�P��ʹ����PAC�����Ϊ6��������ڣ��������P�����ꣻ�������ڣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ���κ���y=ax2+bx+c��ͼ��������˵���У�
��ac��0��
�ڷ���ax2+bx+c=0�ĸ���x1=��1��x2=3��
��a+b+c��0��
�ܵ�x��1ʱ��y����x�����������
��ȷ��˵����________������д��������ȷ����ţ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com