
【题目】如图,点A是反比例函数![]() 图像上的一点,过点A作AB⊥
图像上的一点,过点A作AB⊥![]() 轴于点B,且△AOB的面积为2,点A的坐标为
轴于点B,且△AOB的面积为2,点A的坐标为![]() .
.

(1)求m和k的值.
(2)若一次函数y=ax+3的图像经过点A,交双曲线的另一支于点C,交y轴于点D,求△AOC的面积.
(3)在![]() 轴上是否存在点P,使得△PAC的面积为6?如果存在,请求出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得△PAC的面积为6?如果存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)m=4,k=-4;(2)![]() ;(3)存在,P点坐标为(0,
;(3)存在,P点坐标为(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
试题分析:(1)△AOB的面积为2,点A的坐标为(-1,m)得![]() ,求出m的值,把点A坐标代入
,求出m的值,把点A坐标代入![]() 求得k的值即可;(2)把A(-1,4)代入y=ax+3求出一次函数的表达式,联立
求得k的值即可;(2)把A(-1,4)代入y=ax+3求出一次函数的表达式,联立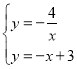 ,解方程组求出点C的坐标,进而求出△AOC的面积;(3)假设存在,设P点坐标为(0,c)有:
,解方程组求出点C的坐标,进而求出△AOC的面积;(3)假设存在,设P点坐标为(0,c)有:![]() =6,进而求出c的值即可.
=6,进而求出c的值即可.
试题解析:(1)依题意得![]() ,∴m=4,∴A(-1,4),把点A(-1,4)代入
,∴m=4,∴A(-1,4),把点A(-1,4)代入![]() 得
得![]() ,∴k=-4,答:m=4,k=-4;
,∴k=-4,答:m=4,k=-4;
(2)把A(-1,4)代入y=ax+3得:4=-a+3,解得a=-1,∴y=-x+3,又∵反比例函数的表达式为![]() ,联立
,联立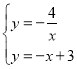 ,解得
,解得![]() ,
,![]() ,∴C的坐标为(4,-1),又当x=0时y=-x+3=-0+3=3,∴OD=3,∴
,∴C的坐标为(4,-1),又当x=0时y=-x+3=-0+3=3,∴OD=3,∴![]() =
=![]() =
=![]() ;
;
(3)答:存在. 理由: 假设存在,设P点坐标为(0,c)有:![]() =6,解得
=6,解得![]() 或
或![]() ,∴P点的坐标为(0,
,∴P点的坐标为(0,![]() )或(0,
)或(0,![]() ), 故存在P点使得△PAC的面积为6.
), 故存在P点使得△PAC的面积为6.


科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
(1)几秒后P,Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1,△ABC的面积为S2,在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3)点B坐标为(2,1);
(2)请作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标;
(3)判断△ABC的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com