
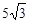 ,那么∠A= ▲ 度.
,那么∠A= ▲ 度. 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源:不详 题型:解答题
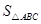 =
=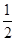 AB·CD,
AB·CD,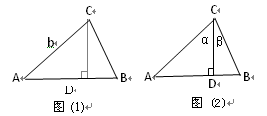
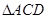 中,
中,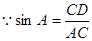 ,
,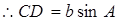
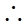
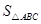 =
=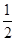 bc·sin∠A.
bc·sin∠A. ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.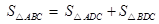 , 由公式①,得
, 由公式①,得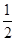 AC·BC·sin(α+β)=
AC·BC·sin(α+β)= 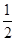 AC·CD·sinα+
AC·CD·sinα+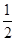 BC·CD·sinβ,
BC·CD·sinβ,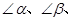
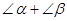 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).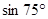 =_________________________
=_________________________查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
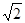 ≈1.414,
≈1.414,
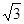 ≈1.732)(7分)
≈1.732)(7分)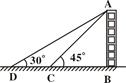
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
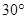 ,此时直升飞机与上海东方明珠底部之间的距离是……………………………………………………( )
,此时直升飞机与上海东方明珠底部之间的距离是……………………………………………………( )A.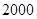 米; 米; | B.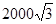 米; 米; | C.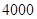 米; 米; | D.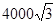 米. 米. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
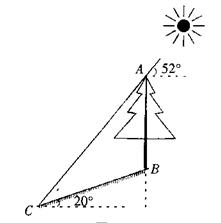
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序:
在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序: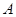 为始点,
为始点,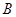 为终点,我们就说线段
为终点,我们就说线段 具有射线的
具有射线的 方向,线段
方向,线段 叫做有向线段,记作
叫做有向线段,记作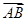 ,线段
,线段 的长度叫做有向线段
的长度叫做有向线段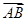 的长度(或模),记作
的长度(或模),记作 。
。
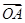 (有向线段与
(有向线段与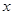 轴的长度单位相同),
轴的长度单位相同), ,
,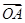 与
与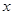 轴的正半轴的夹角是
轴的正半轴的夹角是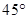 ,且与
,且与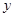 轴的正半轴的夹角是
轴的正半轴的夹角是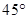 ;
;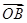 的终点
的终点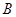 的坐标为(3,
的坐标为(3, ),求它的模及它与
),求它的模及它与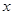 轴的正半轴的夹角
轴的正半轴的夹角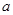 的度数。
的度数。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com