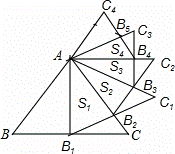
如图.正△ABC的边长为2.以BC边上的高AB1为边作正△AB1C1.△ABC与△AB1C1公共部分的面积记为S1,再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2.△AB1C1与△AB2C2公共部分的面积记为S2,-.以此类推.则Sn= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，正△ABC的边长为2，以BC边上的高AB₁为边作正△AB₁C₁，△ABC与△AB₁C₁公共部分的面积记为S₁；再以正△AB₁C₁边B₁C₁上的高AB₂为边作正△AB₂C₂，△AB₁C₁与△AB₂C₂公共部分的面积记为S₂；…，以此类推，则S_n=　　．（用含n的式子表示）

（）ⁿ

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

设ω是一个平面图形，如果用直尺和圆规经过有限步作图（简称尺规作图），画出一个正方形与ω的面积相等（简称等积），那么这样的等积转化称为ω的“化方”．

⑴阅读填空

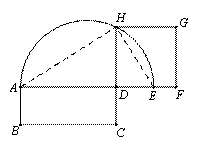
如图①，已知矩形ABCD，延长AD到E，使DE＝DC，以AE为直径作半圆．延长CD交半圆于点H，以DH为边作正方形DFGH，则正方形DFGH与矩形ABCD等积．

理由：连接AH，EH．

∵　AE为直径　　∴　∠AHE＝90°　　∴　∠HAE＋∠HEA＝90°．

∵　DH⊥AE　　∴　∠ADH＝∠EDH＝90°

∴　∠HAD＋∠AHD＝90°

∴　∠AHD＝∠HED　　∴　△ADH∽_____________．

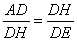∴　，即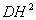＝AD×DE．

又∵　DE＝DC　　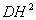∴　＝____________，即正方形DFGH与矩形ABCD等积．

⑵操作实践

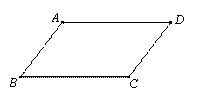
平行四边形的“化方”思路是，先把平行四边形转化为等积的矩形，再把矩形转化为等积的正方形．

如图②，请用尺规作图作出与□ABCD等积的矩形（不要求写具体作法，保留作图痕迹）．

⑶解决问题

三角形的“化方”思路是：先把三角形转化为等积的_________________（填写图形名称），再转化为等积的正方形．

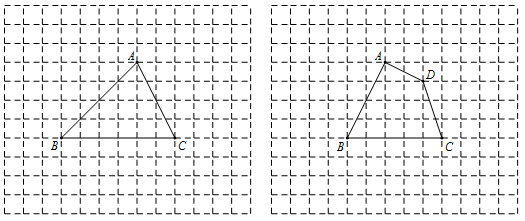
如图③，△ABC的顶点在正方形网格的格点上，请作出与△ABC等积的正方形的一条边（不要求写具体作法，保留作图痕迹，不通过计算△ABC面积作图）．

⑷拓展探究

n边形（n＞3）的“化方”思路之一是：把n边形转化为等积的n－1边形，…，直至转化为等积的三角形，从而可以化方．

如图④，四边形ABCD的顶点在正方形网格的格点上，请作出与四边形ABCD等积的三角形（不要求写具体作法，保留作图痕迹，不通过计算四边形ABCD面积作图）．

查看答案和解析>>

科目：初中数学 来源： 题型：

实数a在数轴的位置如图所示，则|a﹣1|=　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图汽车标志中不是中心对称图形的是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：

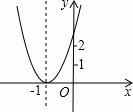
已知二次函数y=ax²+bx+c+2的图象如图所示，顶点为（﹣1，0），下列结论：①abc＜0；②b²﹣4ac=0；③a＞2；④4a﹣2b+c＞0．其中正确结论的个数是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：

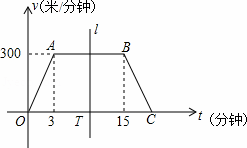
“低碳生活，绿色出行”的理念正逐渐被人们所接受，越来越多的人选择骑自行车上下班．王叔叔某天骑自行车上班从家出发到单位过程中行进速度v（米/分钟）随时间t（分钟）变化的函数图象大致如图所示，图象由三条线段OA、AB和BC组成．设线段OC上有一动点T（t，0），直线l左侧部分的面积即为t分钟内王叔叔行进的路程s（米）．