
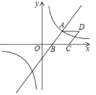
【题目】如图,已知一次函数 y=![]() x﹣3 与反比例函数 y=
x﹣3 与反比例函数 y=![]() 的图象相交于点 A(4,n),与 x 轴相交于点 B.
的图象相交于点 A(4,n),与 x 轴相交于点 B.
(1)求 n 与 k 的值;
(2)以 AB 为边作菱形 ABCD,使点 C 在 x 轴正半轴上,点 D 在第一象限,求点 D 的坐标;
(3)观察反比例函数y=![]() 的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.
的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.
【答案】(1)n=3,k=12;(2)D(4+![]() ,3);(3) x<﹣6 或 x>0.
,3);(3) x<﹣6 或 x>0.
【解析】
(1)因为点![]() 在一次函数y=
在一次函数y=![]() x﹣3 的图象上,所以
x﹣3 的图象上,所以![]() ,又因为点
,又因为点![]() 在反比例函数
在反比例函数![]() 图象上,所以k=12.
图象上,所以k=12.
(2)首先根据直线方程求出点B的坐标,再由勾股定理求出菱形边长,再由菱形性质得知四边相等,最后根据平移性质的关系即可写出点![]() 的坐标.
的坐标.
(3)根据反比函数的性质即可得到当y>-2时,自变量x的取值范围.
解:(1)把 A 点坐标代入一次函数解析式可得 n=![]() ×4﹣3=3,
×4﹣3=3,
∴A(4,3),
∵A 点在反比例函数图象上,
∴k=3×4=12;
(2)在 y=![]() x﹣3 中,令 y=0 可得 x=2,
x﹣3 中,令 y=0 可得 x=2,
∴B(2,0),
∵A(4,3),
∴AB=![]() ,
,
∵四边形 ABCD 为菱形,且点 C 在 x 轴正半轴上,点 D 在第一象限,
∴BC=AB=![]() ,
,
∴点 C 由点 B 向右平移![]() 个单位得到,
个单位得到,
∴点 D 由点 A 向右平移![]() 个单位得到,
个单位得到,
∴D(4+![]() ,3);
,3);
(3)由(1)可知反比例函数解析式为 y=![]() , 令 y=﹣2 可得 x=﹣6,
, 令 y=﹣2 可得 x=﹣6,
结合图象可知当 y>﹣2 时,x 的取值范围为 x<﹣6 或 x>0.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: ![]()
![]()
![]()
![]()
![]() 以上这种化简的步骤叫做分母有理化.
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求 a2 b2 .我们可以把ab和ab看成是一个整体,令 xab , y ab ,则 a 2 b2 (a b)2 2ab x2 2y 4 610.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算:![]()
![]()
![]()
![]()
(2)已知 m 是正整数, a ![]() ,b
,b ![]() 且 2a2 1823ab 2b2 2019 .求 m.
且 2a2 1823ab 2b2 2019 .求 m.
(3)已知![]() ,则
,则![]() 的值为
的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求sin∠F.

查看答案和解析>>
科目:初中数学 来源: 题型:
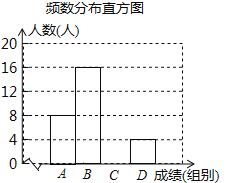
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
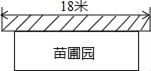
【题目】晨光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围;
(2)设这个苗圃园的面积为S,求S与x之间的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面从认知、延伸、应用三个层面来研究一种几何模型.
(1)如图,已知点E是线段BC上一点,若∠AED=∠B=∠C.求证 △ABE∽△ECD.

(2)如图,已知点E、F是线段BC上两点,AE与DF交于点H,若∠AHD=∠B=∠C.
求证:△ABE∽△FCD.

(3)如图,⊙O是等边△ABC的外接圆,点D是![]() 上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.
上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是

A、当弦PB最长时,ΔAPC是等腰三角形 B、当ΔAPC是等腰三角形时,PO⊥AC
C、当PO⊥AC时,∠ACP=300 D、当∠ACP=300时,ΔPBC是直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com