
【题目】阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: ![]()
![]()
![]()
![]()
![]() 以上这种化简的步骤叫做分母有理化.
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求 a2 b2 .我们可以把ab和ab看成是一个整体,令 xab , y ab ,则 a 2 b2 (a b)2 2ab x2 2y 4 610.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算:![]()
![]()
![]()
![]()
(2)已知 m 是正整数, a ![]() ,b
,b ![]() 且 2a2 1823ab 2b2 2019 .求 m.
且 2a2 1823ab 2b2 2019 .求 m.
(3)已知![]() ,则
,则![]() 的值为
的值为
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
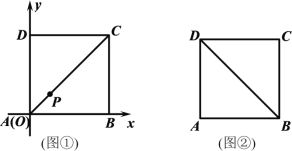
【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=![]() 时,求点P的坐标;
时,求点P的坐标;
(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
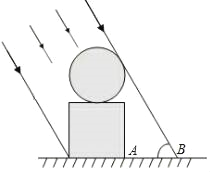
【题目】如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
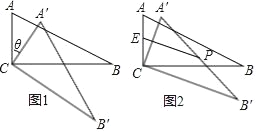
【题目】在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A'B'C.
(1)如图1,当AB∥CB'时,设A'B'与CB相交于点D,求证:△A'CD是等边三角形.
(2)若E为AC的中点,P为A'B'的中点,则EP的最大值是多少,这时旋转角θ为多少度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
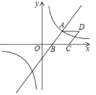
【题目】如图,已知一次函数 y=![]() x﹣3 与反比例函数 y=
x﹣3 与反比例函数 y=![]() 的图象相交于点 A(4,n),与 x 轴相交于点 B.
的图象相交于点 A(4,n),与 x 轴相交于点 B.
(1)求 n 与 k 的值;
(2)以 AB 为边作菱形 ABCD,使点 C 在 x 轴正半轴上,点 D 在第一象限,求点 D 的坐标;
(3)观察反比例函数y=![]() 的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.
的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com