
【题目】如图所示:已知∠ABC=120°,作等边△ACD,将△ACD旋转60°,得到△CDE,AB=3,BC=2,求BD和∠ABD.
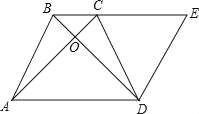
【答案】BD=5.∠BAD=60°
【解析】
先根据等边三角形的性质得∠ADC=∠ACD=60°,由于∠ABC=120°,根据四边形内角和得到∠BAD+∠BCD=180°,则∠BAD+∠BCA=120°,再根据旋转的性质得∠BAD=∠ECD,DB=DE,∠BDE=60°,AB=CE,于是有∠BCA+∠ECD+∠ACD=180°,得到B、C、E在同一条直线上,接着证明△BDE为等边三角形得到∠DBE=60°,所以∠BAD=∠ABC﹣∠DBE=60°,BD=BE=BC+CE=BC+AB=5.
∵△ACD是等边三角形,
∴∠ADC=∠ACD=60°,
∵∠ABC=120°,
∴∠BAD+∠BCD=180°,
∴∠BAD+∠BCA=120°,
∵△ABD绕点D按顺时针方向旋转60°后到△ECD的位置,
∴∠BAD=∠ECD,DB=DE,∠BDE=60°,AB=CE,
∴∠BCA+∠ECD=120°,
∴∠BCA+∠ECD+∠ACD=180°,
∴B、C、E在同一条直线上.
∵DB=DE,∠BDE=60°,
∴△BDE为等边三角形,
∴∠DBE=60°,
∴∠BAD=∠ABC﹣∠DBE=60°,
∴BD=BE=BC+CE=BC+AB=3+2=5.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:
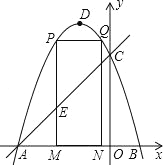
【题目】如图,抛物线 y=﹣x2﹣2x+3 的图象与 x 轴交于 A、B 两点(点 A 在点 B 的左边),与 y轴交于点 C,点 D 为抛物线的顶点.
(1)求点 A、B、C 的坐标;
(2)点 M(m,0)为线段 AB 上一点(点 M 不与点 A、B 重合),过点 M 作 x 轴的垂线,与直线 AC 交于点 E,与抛物线交于点 P,过点 P 作 PQ∥AB 交抛物线于点 Q,过点 Q 作 QN⊥x 轴于点 N,可得矩形 PQNM.如图,点 P 在点 Q 左边,试用含 m 的式子表示矩形 PQNM 的周长;
(3)当矩形 PQNM 的周长最大时,m 的值是多少?并求出此时的△AEM 的面积;
(4)在(3)的条件下,当矩形 PMNQ 的周长最大时,连接 DQ,过抛物线上一点 F 作 y 轴的平行线,与直线 AC 交于点 G(点 G 在点 F 的上方).若 FG=2![]() DQ,求点 F 的坐标.
DQ,求点 F 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
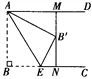
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
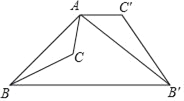
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:![]() .唐诗;
.唐诗;![]() .宋词;
.宋词;![]() .论语;
.论语;![]() .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+2
x+2![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
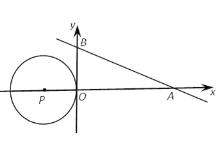
A. 3 B. 4 C. 5 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:y=ax2-4ax+3a-2(a≠0),其顶点为C,直线l:y=ax-2a+1(a≠0)与x轴、y轴分别交于A,B两点.
(1)当抛物线G的顶点C在x轴上时,求a的值;
(2)当a>0时,若△ABC的面积为2,求a的值;
(3)若点Q(m,n)在抛物线G上,把抛物线G绕着点P(t,-2)旋转180°,在1≤m≤3时,总有n随着m的增大而增大,请直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: ![]()
![]()
![]()
![]()
![]() 以上这种化简的步骤叫做分母有理化.
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求 a2 b2 .我们可以把ab和ab看成是一个整体,令 xab , y ab ,则 a 2 b2 (a b)2 2ab x2 2y 4 610.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算:![]()
![]()
![]()
![]()
(2)已知 m 是正整数, a ![]() ,b
,b ![]() 且 2a2 1823ab 2b2 2019 .求 m.
且 2a2 1823ab 2b2 2019 .求 m.
(3)已知![]() ,则
,则![]() 的值为
的值为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com