
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
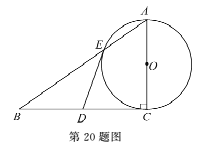
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学习了四边形和一些特殊的四边形,如图表示了在某种条件下它们之间的关系.如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行.那么请你对标上的其他6个数字序号写出相对应的条件. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
查看答案和解析>>
科目:初中数学 来源: 题型:
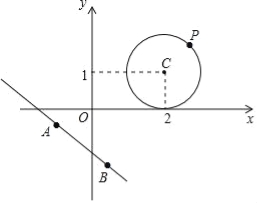
【题目】阅读材料:
在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0的距离公式为:d=![]() .
.
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d=![]() =
=![]() .
.
根据以上材料,解决下列问题:
问题1:点P1(3,4)到直线y=﹣![]() x+
x+![]() 的距离为 ;
的距离为 ;
问题2:已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣![]() x+b相切,求实数b的值;
x+b相切,求实数b的值;
问题3:如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论: ①EG=FG;②∠ABG=60°;③AE=1;④△BEF是等边三角形;其中正确结论的序号是 . 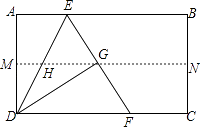
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校后勤人员到一家文具店给九年级的同学购买考试用文具包,文具店规定一次购买400个以上,可享受8折优惠.若给九年级学生每人购买一个,不能享受8折优惠,需付款1936元;若多买88个,就可享受8折优惠,同样只需付款1936元.请问该学校九年级学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com