
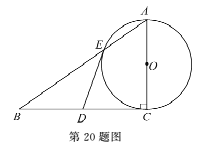
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】:
试题分析:利用思路:知(连)半径,证垂直,证明DE是圆O的切线;利用射影定理或相似三角形证明:BE2=BE×BA,再列方程,求AE的长.
试题解析:(1)如图所示,连接OE,CE
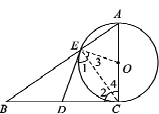
∵AC是圆O的直径
∴∠AEC=∠BEC=90°
∵D是BC的中点
∴ED=![]() BC=DC
BC=DC
∴∠1=∠2
∵OE=OC
∴∠3=∠4
∴∠1+∠3=∠2+∠4,即∠OED=∠ACD
∵∠ACD=90°
∴∠OED=90°,即OE⊥DE
又∵E是圆O上的一点
∴DE是圆O的切线.
(2)由(1)知∠BEC=90°
在RtΔBEC与RtΔBCA中,∠B为公共角,
∴ΔBEC∽ΔBCA
∴![]()
即BC2=BE×BA
∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x.
又∵BC=6
∴62=2x×3x
∴x=![]() ,即AE=
,即AE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】由于受H7N9禽流感的影响,今年4月份鸡的价格两次大幅下降.由原来每斤12元连续两次降价a%后售价下调到每斤5元,下列所列方程中正确的是( )
A.12(1+a%)2=5
B.12(1﹣a%)2=5
C.12(1﹣2a%)=5
D.12(1﹣a2%)=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠ACB=25°,现将ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( ) 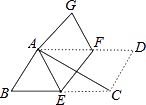
A.135°
B.120°
C.115°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式能用平方差公式计算的是( )
A.(2a+b)(2b﹣a)
B.(x+1)(﹣x﹣1)
C.(﹣m﹣n)(﹣m+n)
D.(3x﹣y)(﹣3x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条平行线间的距离公式 一般地;两条平行线l1:Ax+By+C1=0和l2:Ax+By+C2=0间的距离公式是d= ![]() 如:求:两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离.
如:求:两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离.
解:将两方程中x,y的系数化成对应相等的形式,得2x+6y﹣8=0和2x+6y﹣9=0,因此,d= ![]() 两条平行线l1:3x+4y=10和l2:6x+8y﹣10=0的距离是 .
两条平行线l1:3x+4y=10和l2:6x+8y﹣10=0的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com