
【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】巴中市某楼盘准备以每平方米5000元的均价对外销售,由于有关部门关于房地产的新政策出台后,部分购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4050元的均价开盘销售,若两次下调的百分率相同,求平均每次下调的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取范围内最大整数时函数的解析式;
取范围内最大整数时函数的解析式;
(2)题(1)中求得的函数记为C1
①当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
②函数C2:![]() 的图象由函数C1的图象平移得到,其顶点P落在以原
的图象由函数C1的图象平移得到,其顶点P落在以原
点为圆心,半径为![]() 的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距
的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距
离最大时函数C2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.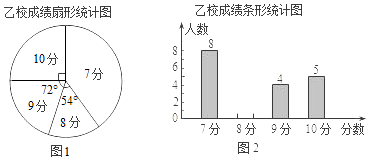
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 |
(1)在图1中,“7分”所在扇形的圆心角等于°.
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( ) 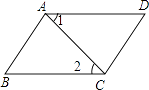
A.AB=DC
B.∠1=∠2
C.AB=AD
D.∠D=∠B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com