
【题目】阅读材料:
在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0的距离公式为:d=![]() .
.
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d=![]() =
=![]() .
.
根据以上材料,解决下列问题:
问题1:点P1(3,4)到直线y=﹣![]() x+
x+![]() 的距离为 ;
的距离为 ;
问题2:已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣![]() x+b相切,求实数b的值;
x+b相切,求实数b的值;
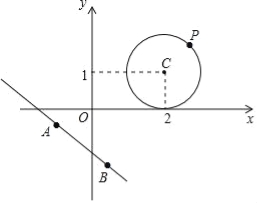
问题3:如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.
【答案】(1)4;(2)b=5或15;(3)最大值为4,最小值为2.
【解析】试题分析:(1)根据点到直线的距离公式就是即可;(2)根据点到直线的距离公式,列出方程即可解决问题;(3)求出圆心C到直线3x+4y+5=0的距离,求出⊙C上点P到直线3x+4y+5=0的距离的最大值以及最小值即可解决问题.
试题解析:
(1)点P1(3,4)到直线3x+4y﹣5=0的距离d=![]() =4;
=4;
(2)∵⊙C与直线y=﹣![]() x+b相切,⊙C的半径为1,
x+b相切,⊙C的半径为1,
∴C(2,1)到直线3x+4y﹣b=0的距离d=1,
∴![]() =1,
=1,
解得b=5或15.
(3)点C(2,1)到直线3x+4y+5=0的距离d=![]() =3,
=3,
∴⊙C上点P到直线3x+4y+5=0的距离的最大值为4,最小值为2,
∴S△ABP的最大值=![]() ×2×4=4,S△ABP的最小值=
×2×4=4,S△ABP的最小值=![]() ×2×2=2.
×2×2=2.


科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取范围内最大整数时函数的解析式;
取范围内最大整数时函数的解析式;
(2)题(1)中求得的函数记为C1
①当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
②函数C2:![]() 的图象由函数C1的图象平移得到,其顶点P落在以原
的图象由函数C1的图象平移得到,其顶点P落在以原
点为圆心,半径为![]() 的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距
的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距
离最大时函数C2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.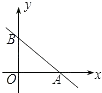
(1)求函数y= ![]() x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;
(2)若函数y= ![]() x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算中,不正确的是( )
A.﹣2x+3x=x
B.6xy2÷2xy=3y
C.(﹣2x2y)3=﹣6x6y3
D.2xy2(﹣x)=﹣2x2y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com