
【题目】如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:![]() ≈1.73)
≈1.73)
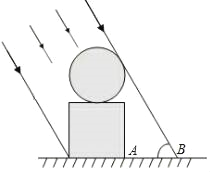
【答案】雕塑的高度为4.24米.
【解析】
先过D作DF⊥AB于F,过O作OG⊥AB于G,过O作DF的垂线,交DF于H,交⊙O于E,则AE为⊙O的切线,延长AE交BD于C,设⊙O的半径为r,则OG= 3r=HF=AE,OD=r,根据∠ACB=30°,∠DOE=30°,得到Rt△ODH中,DH=![]() OD=
OD=![]() r,DF=
r,DF=![]() r+3r,进而得出CE=CD=AC-AE=2
r+3r,进而得出CE=CD=AC-AE=2![]() -3r,再根据AC∥DF,得出
-3r,再根据AC∥DF,得出![]() ,进而求得r≈1.06,据此可得这个雕塑的高度.
,进而求得r≈1.06,据此可得这个雕塑的高度.
如图所示,设D为光线与⊙O的切点,过D作DF⊥AB于F,过O作OG⊥AB于G,
过O作DF的垂线,交DF于H,交⊙O于E,
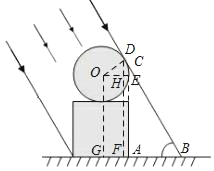
则AE为⊙O的切线,延长AE交BD于C,
设⊙O的半径为r,则OG=3r=HF=AE,OD=r,
∵∠ABD=60°,
∴∠ACB=30°,∠DOE=30°,
∴Rt△ODH中,DH=![]() OD=
OD=![]() r,
r,
∴DF=![]() r+3r,
r+3r,
又∵Rt△ABC中,AB=2,
∴AC=2![]() ,BC=4,
,BC=4,
∴CE=CD=AC﹣AE=2![]() ﹣3r,
﹣3r,
∵AC∥DF,
∴![]() ,即,
,即,![]()
解得r≈1.06,
∴雕塑的高度为4r=4×1.06=4.24米.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:![]() .唐诗;
.唐诗;![]() .宋词;
.宋词;![]() .论语;
.论语;![]() .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: ![]()
![]()
![]()
![]()
![]() 以上这种化简的步骤叫做分母有理化.
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求 a2 b2 .我们可以把ab和ab看成是一个整体,令 xab , y ab ,则 a 2 b2 (a b)2 2ab x2 2y 4 610.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算:![]()
![]()
![]()
![]()
(2)已知 m 是正整数, a ![]() ,b
,b ![]() 且 2a2 1823ab 2b2 2019 .求 m.
且 2a2 1823ab 2b2 2019 .求 m.
(3)已知![]() ,则
,则![]() 的值为
的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
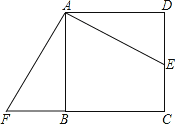
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
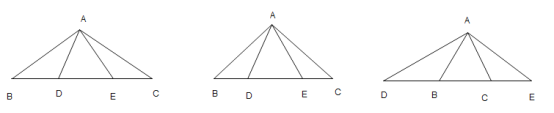
【题目】等腰直角三角形 ABC 中,BAC 90° ,AB AC 6 ![]() ,D,E 是线段 BC 上的动点,且 DAE 45°
,D,E 是线段 BC 上的动点,且 DAE 45°
(1)如图 1,请直接写出 BD,DE,EC 满足的关系式为 ,
(2)①如图 1, CE 3 ,请求出 ADE 的面积(写出过程);
②如图 2, EAC 30° ,请求出 CE 的长度(写出过程);
(3) 如图 3,D,E 运动到了线段的延长线上,且满足 DAE 135°,CE=8,直接写出 BD的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
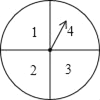
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
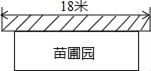
【题目】晨光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围;
(2)设这个苗圃园的面积为S,求S与x之间的函数关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com