
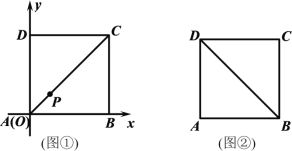
【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=![]() 时,求点P的坐标;
时,求点P的坐标;
(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:y=ax2-4ax+3a-2(a≠0),其顶点为C,直线l:y=ax-2a+1(a≠0)与x轴、y轴分别交于A,B两点.
(1)当抛物线G的顶点C在x轴上时,求a的值;
(2)当a>0时,若△ABC的面积为2,求a的值;
(3)若点Q(m,n)在抛物线G上,把抛物线G绕着点P(t,-2)旋转180°,在1≤m≤3时,总有n随着m的增大而增大,请直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点C、D在线段AB上,若点C是线段AD的中点,2BD>AD,则下列结论正确的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: ![]()
![]()
![]()
![]()
![]() 以上这种化简的步骤叫做分母有理化.
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求 a2 b2 .我们可以把ab和ab看成是一个整体,令 xab , y ab ,则 a 2 b2 (a b)2 2ab x2 2y 4 610.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算:![]()
![]()
![]()
![]()
(2)已知 m 是正整数, a ![]() ,b
,b ![]() 且 2a2 1823ab 2b2 2019 .求 m.
且 2a2 1823ab 2b2 2019 .求 m.
(3)已知![]() ,则
,则![]() 的值为
的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
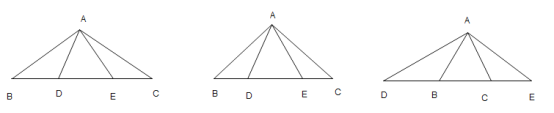
【题目】等腰直角三角形 ABC 中,BAC 90° ,AB AC 6 ![]() ,D,E 是线段 BC 上的动点,且 DAE 45°
,D,E 是线段 BC 上的动点,且 DAE 45°
(1)如图 1,请直接写出 BD,DE,EC 满足的关系式为 ,
(2)①如图 1, CE 3 ,请求出 ADE 的面积(写出过程);
②如图 2, EAC 30° ,请求出 CE 的长度(写出过程);
(3) 如图 3,D,E 运动到了线段的延长线上,且满足 DAE 135°,CE=8,直接写出 BD的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
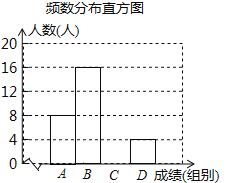
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com