
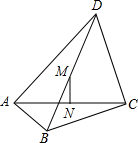
 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=12,CD=AC=16,M、N分别是对角线BD、AC的中点.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=12,CD=AC=16,M、N分别是对角线BD、AC的中点.分析 (1)连接AM、CM,根据直角三角形斜边上的中线等于斜边的一半可得AM=CM=BM=DM=$\frac{1}{2}$BD,再根据等腰三角形三线合一的性质证明;
(2)利用勾股定理类似求出BD,再求出AM、AN,再利用勾股定理列式计算即可得解.
解答 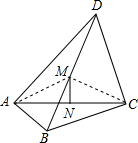 (1)证明:如图,连接AM、CM,
(1)证明:如图,连接AM、CM,
∵∠BAD=∠BCD=90°,M是BD的中点,
∴AM=CM=BM=DM=$\frac{1}{2}$BD,
∵N是AC的中点,
∴MN⊥AC;
(2)解:∵∠BCD=90°,BC=12,CD=16,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=20,
∴AM=$\frac{1}{2}$×20=10,
∵AC=16,N是AC的中点,
∴AN=$\frac{1}{2}$×16=8,
∴MN=$\sqrt{A{M}^{2}-A{N}^{2}}$=8.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,勾股定理,熟记性质与定理并作辅助线构造出等腰三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
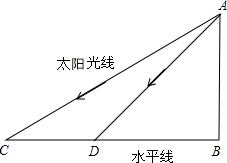 在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)
在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com