
����Ŀ����֪��A��a��0����B��0��b������![]() ���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-B-C-A-O��·���ƶ���
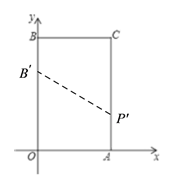
���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-B-C-A-O��·���ƶ���
��1��д��A��B��C��������ꣻ
��2������P�ƶ���6��ʱ�������ʱP���λ�ã���д����P��λ�����ꣻ
��3�����ᣨ2����B��P���㣬���߶�BP����ƽ��h����λ��h��0�����õ�B��P�䣬��B��P�佫�ı���OACB���ܳ��ֳ���ȵ������֣���h��ֵ��

���𰸡���1��A��4��0����B��0��6����C��4��6������2��P��4��4������3��h��ֵΪ2��
�����������������
��1����![]() �ɽ����a=4��b=6���Ӷ��ɵõ�A��B������ֱ�Ϊ��4��0���ͣ�0��6�����������ɵõ�C������Ϊ��4��6����
�ɽ����a=4��b=6���Ӷ��ɵõ�A��B������ֱ�Ϊ��4��0���ͣ�0��6�����������ɵõ�C������Ϊ��4��6����
��2���������֪��6��ʱ����P�˶���12����λ���ȣ��ɵ�A��B��C������ɵ�OA=BC=4��AC=OB=6���ɴ˼��ɵõ���P������Ϊ��4��4����
��3������ͼ����OB��+AP��=![]() (OB+AC)ʱ��BPƽ���ı���OACBA���ܳ����ɴ˸�������ɵã�6-h+6-2-h=6�����h=2.
(OB+AC)ʱ��BPƽ���ı���OACBA���ܳ����ɴ˸�������ɵã�6-h+6-2-h=6�����h=2.
���������
��1����![]() ��
��
��a-4=0��b-6=0�����a=4��b=6��
����A��B������ֱ�Ϊ��4��0���ͣ�0��6����
����C��������4��6����
��2���ߵ�Pÿ���ƶ�6����λ���ȣ�
��6��ʱ����P�ƶ���12����λ���ȣ�
��OA=BC=4��AC=OB=6��
����6��ʱ����P������Ϊ��4��4����
��3������ͼ��ʾ��������ɵõ�OB��+AP��=![]() (OB+AC)ʱ��BPƽ���ı���OACBA���ܳ���
(OB+AC)ʱ��BPƽ���ı���OACBA���ܳ���
��6-h+6-2-h=6�����h=2.
����h=2ʱ��B��P��ƽ���ı���OABC���ܳ�.


 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�ǡ�ABC�У���AΪֱ�ǣ�AB=6��AC=8����P��Q��R�ֱ���AB��BC��CA����ͬʱ��ʼ�������˶���2���������ͬʱֹͣ�˶�����P�ɵ�A������ÿ��3����λ���ٶ����B�˶�����Q�ɵ�B������ÿ��5����λ���ٶ����C�˶�����R�ɵ�C������ÿ��4����λ���ٶ����A�˶������˶������У�
��1����֤����APR����BPQ����CQR�������ȣ�
��2�����PQR�������Сֵ��
��3����t���룩��0��t��2����ʾ�˶�ʱ�䣬�Ƿ����t��ʹ��PQR=90�㣿�����ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ岻����ƴ���Ľ��ǣ� ��
A. 105�� B. 75�� C. 85�� D. 15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
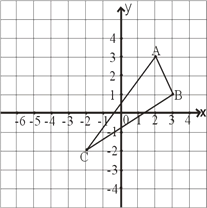
����Ŀ����ͼ����֪��ABC����������ֱ�ΪA��2��3����B��3��1����C����2����2��.
��1������ͼ��������ABC����y��Գ�ͼ����DEF��A��B��C�Ķ�Ӧ��ֱ���D��E��F������ֱд��D��E��F������.D��E��F��������ǣ�D( , ) E( , ) F( , )��
��2�����ı���ABED�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����O����ABC������AB��AC����ֱ�ߵľ���OD=OE����OB��OC.
��1����ͼ������O��BC�ϣ���֤��AB��AC��
��2����ͼ������O����ABC���ڲ�����֤��AB��AC��
��3������O����ABC���ⲿ��AB��AC�������뻭ͼ��ʾ.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���ij����Ʒ�������ۣ���x������۵���ΪmԪ/������������Ϊn��������m��n�ֱ���x��1��x��30����xΪ��������һ�κ���������������±���

��1�����̱������ݣ��ֱ�ֱ��д��m��x��n��x�ĺ�����ϵʽ�� �� ��
��2�����̳����۸���Ʒ�ڼ���ʱ����Ʒ�������۶�ǡ��Ϊ3600Ԫ��
��3��������Ʒ�ĵ�15��Ϊ��ͯ�ڣ����ʣ��ڶ�ͯ��ǰ����������ͯ�ڵ��죩���۸���Ʒ�ڼ���ʱ����Ʒ�������۶���ࣿ�̳��������������Ʒ�������۶������ͯ����Ժ��������̳��ɾ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У�����������ǣ�������
A.�������ǿ�������������
B.y ���ϵĵ㣬������Ϊ 0
C.�ڲ���һ������
D.����ֻ��һ��ֱ������ֱ֪�ߴ�ֱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ������CB��OA����C=��OAB=100�㣬E��F��CB�ϣ��������FOB=��AOB��OEƽ�֡�COF��
��1�����EOB�Ķ�����
��2����ƽ���ƶ�AB����ô��OBC�á�OFC��ֵ�Ƿ���֮�仯�����仯���ҳ��仯���ɣ������䣬��������ֵ��
��3����ƽ���ƶ�AB�Ĺ����У��Ƿ����ij�������ʹ��OEC=��OBA�������ڣ������������������ڣ�˵�����ɡ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com