
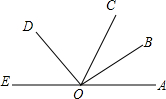
 如图,已知OB是∠AOC平分线,OD是∠COE平分线,∠COD=2∠AOB.
如图,已知OB是∠AOC平分线,OD是∠COE平分线,∠COD=2∠AOB.分析 (1)根据角平分线的定义可得∠BOC=$\frac{1}{2}$∠AOC,∠DOC=$\frac{1}{2}$∠COE,则∠BOC+∠DOC=$\frac{1}{2}$(∠AOC+∠COE),根据平角的定义可求∠DOB的度数,再根据∠COD=2∠AOB=2∠BOC,可求∠AOB的度数;
(2)根据若两个角的和为90°,则这两个角互余,可求∠COD余角的度数;
(3)若两个角的和等于180°,则这两个角互补,可求∠DOE补角的度数.
解答 解:(1)∵OB是∠AOC平分线,OD是∠COE平分线,
∴∠BOC=$\frac{1}{2}$∠AOC,∠DOC=$\frac{1}{2}$∠COE,
∴∠BOC+∠DOC=$\frac{1}{2}$(∠AOC+∠COE),
∴∠DOB=90°,
∵∠COD=2∠AOB=2∠BOC,
∴∠AOB=90°×$\frac{1}{3}$=30°;
(2)∵∠COD=90°-∠BOC=60°,
∴∠COD余角的度数是90°-60°=30°;
(3)∵∠DOE=∠COD=60°,
∴∠DOE补角的度数是180°-60°=120°.
点评 此题综合考查角平分线,余角和补角,较难.在找互补或互余的两角时,可先确定较小(或较大)角的度数,从最小(或最大)角的补角(或余角)开始找,能做到不重合、不遗漏.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
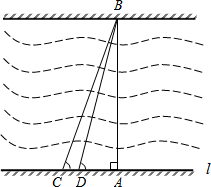 某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.
某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
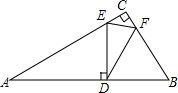 如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD=$\frac{6}{5}$或$\frac{4}{3}$.
如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD=$\frac{6}{5}$或$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-2,-3) | C. | (3,-2) | D. | (3,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com