Question

18．如图，⊙O的直径AB=4，AC是弦，将⊙O沿AC折叠，折叠后$\widehat{AC}$交AB于点D．
（1）设BD=x，用关于x的代数式表示弦AC的长．
（2）若要使$\widehat{CD}$=60°，求BD的长．

Answer 1

分析 （1）作辅助线，构建一个新的圆P，与圆O是等圆，则半径相等为2，根据勾股定理表示PH、OH、OP的长，再证明△ACB∽△PHO，得$\frac{AC}{PH}=\frac{AB}{PO}$，代入可求得结论；
（2）根据弧的度数是所对圆心角的度数，得圆周角∠CAB=30°，根据特殊的三角函数值列式求得x的长．

解答 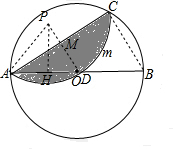解：（1）设折叠后的$\widehat{AmC}$的圆心为P，
由折叠得：⊙O与⊙P是等圆，
∴AP=$\frac{1}{2}$AB=2，
∵BD=x，则AD=4-x，
∴AH=DH=$\frac{4-x}{2}$=2-$\frac{x}{2}$，OH=OA-AH=2-（2-$\frac{x}{2}$）=$\frac{x}{2}$，
过P作PH⊥AB于H，连接PO、BC、PC、PA，
∴PH²=PA²-AH²=2²-（2-$\frac{x}{2}$）²=2x-$\frac{1}{4}{x}^{2}$，
OP²=$\frac{1}{4}{x}^{2}$+2x-$\frac{1}{4}{x}^{2}$=2x，
∵OP⊥AC，
∴∠PMA=90°，
∴∠PMA=∠AHP，
∴∠BAC=∠HPO，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠ACB=∠PHO，
∴△ACB∽△PHO，
∴$\frac{AC}{PH}=\frac{AB}{PO}$，
∴$\frac{AC}{\sqrt{2x-\frac{1}{4}{x}^{2}}}$=$\frac{4}{\sqrt{2x}}$，
∴AC=$\sqrt{16-2x}$；
（2）当$\widehat{CD}$=60°时，∠CAB=30°，
cos30°=$\frac{AM}{AO}$，
$\frac{\sqrt{3}}{2}$=$\frac{\frac{\sqrt{16-2x}}{2}}{2}$，
x=2，
∴BD=2．

点评 本题是折叠问题，折叠前后的图形全等，则新的圆P与圆O是等圆，根据勾股定理和半径的关系列式，又利用了垂径定理：垂直于弦的直径平分弦且平分弦所对的两条弧；及它得出的推论，要熟练掌握，在圆的证明中经常运用；本题与三角函数结合使问题得以解决．