
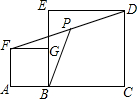
 如图,点A、B在一直线上,以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE,点P是DF的中点,连结BP.已知AB=3cm,BC=9cm,则BP的值是( )
如图,点A、B在一直线上,以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE,点P是DF的中点,连结BP.已知AB=3cm,BC=9cm,则BP的值是( )| A. | 6cm | B. | $\frac{3\sqrt{13}}{2}$cm | C. | 4$\sqrt{3}$cm | D. | 3$\sqrt{5}$cm |
科目:初中数学 来源: 题型:解答题
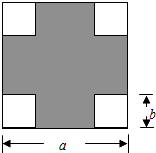 如图,在一块边长为a的正方形纸板的四周,各剪去一个边长为b(b<$\frac{a}{2}$)的正方形.
如图,在一块边长为a的正方形纸板的四周,各剪去一个边长为b(b<$\frac{a}{2}$)的正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
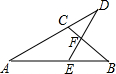 如图,在△ABC中,D是AC延长线上的一点,E是AB上的一点,连接DE交BC于点F,已知∠A=27°,∠EFB=85°,∠B=38°,求∠D和∠DEB的度数.
如图,在△ABC中,D是AC延长线上的一点,E是AB上的一点,连接DE交BC于点F,已知∠A=27°,∠EFB=85°,∠B=38°,求∠D和∠DEB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
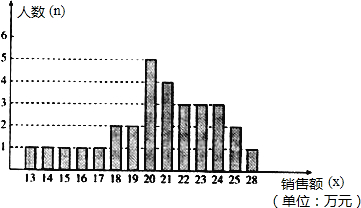
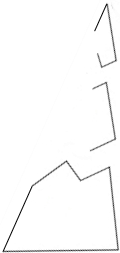 课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么?
课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com