
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
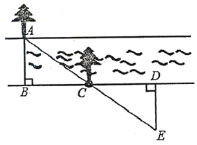
①在河流的一侧岸边B点,选对岸正对的一棵树A;
②沿河岸直走20米有一树C,继续前行20米到达D处;
③从D处沿与河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求河流的宽度是多少?并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费![]() 自来水销售费用
自来水销售费用![]() 污水处理费用)
污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 |
| 0.80 |
超过17吨不超过30吨的部分 |
| 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求![]() ,
,![]() 的值.
的值.
(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCO的边长为3,点O为坐标原点,点A、C分别在x轴、y轴上,点B在第一象限内直线y=kx+1分别与x轴、y轴、线段BC交于点F、D、G,AE⊥FG,下列结论:①△GCD和△FOD的面积比为3:1:②AE的最大长度为![]() :③tan∠FEO=
:③tan∠FEO=![]() ④当DA平分∠EAO时,CG=
④当DA平分∠EAO时,CG=![]() ,其中正确的结论有( )
,其中正确的结论有( )

A. ①②③ B. ②③ C. ②③④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆出租车计费的方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车起步价是_____元;
(2)当x>2时,求y与x之间的关系式;
(3)若某乘客一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点开始沿一条东西方向的直线爬行,规定以出发点为原点,向东爬行的路程记为正数,向西爬行的路程记为负数,则蜗牛爬过的各段路程依次为+5,-3,+10,-8,-6,+12,-10.(单位:厘米)
(1)请判断蜗牛最后是否回到出发点?
(2)蜗牛离开出发点0最远时是多少厘米?
(3)在爬行过程中,若蜗牛每爬1厘米就奖励一粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 为直线
为直线![]() 上的一点,
上的一点,![]() 为直角,
为直角,![]() 平分
平分![]() .
.
(1)如图1,若![]() ,则
,则![]() ______°.
______°.
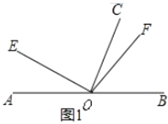
(2)如图1,若![]() ,求
,求![]() 的度数.(用含
的度数.(用含![]() 的代数式表示)
的代数式表示)
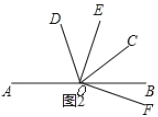
(3)如图2,若![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 |
|
二 |
| 10 | 0.2 |
三 |
| 12 |
|
四 |
|
| 0.4 |
五 |
| 6 |
|

请根据表格提供的信息,解答以下问题:
(1)本次决赛共有__________名学生参加;
(2)直接写出表中:![]() ___________
___________![]() ____________
____________
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=75°,BC=7,△ABC的面积为14,D为 BC边上一动点(不与B,C重合),将△ABD和△ACD分别沿直线AB,AC翻折得到△ABE与△ACF,那么△AEF的面积最小值为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com