
【题目】如图,在平面直角坐标系中,正方形ABCO的边长为3,点O为坐标原点,点A、C分别在x轴、y轴上,点B在第一象限内直线y=kx+1分别与x轴、y轴、线段BC交于点F、D、G,AE⊥FG,下列结论:①△GCD和△FOD的面积比为3:1:②AE的最大长度为![]() :③tan∠FEO=
:③tan∠FEO=![]() ④当DA平分∠EAO时,CG=
④当DA平分∠EAO时,CG=![]() ,其中正确的结论有( )
,其中正确的结论有( )

A. ①②③ B. ②③ C. ②③④ D. ③④
【答案】C
【解析】分析:令x=0,得y=1,得OD=1,由OD=1得CD=2,易证△GCD∽△FOD,从而可得△GCD和△FOD的面积比为4:1,故①错误;由勾股定理和三角形三边关系可得AE的最大长度为![]() ,故②正确;由OD⊥OA,AE⊥DE得A、O、D、E四点共圆,由∠FEO+∠OEA=90°,∠ODA+∠OAD=90°,∠OEA=∠ODA得∠FEO=∠ODA故tan∠FEO=tan∠ODA=
,故②正确;由OD⊥OA,AE⊥DE得A、O、D、E四点共圆,由∠FEO+∠OEA=90°,∠ODA+∠OAD=90°,∠OEA=∠ODA得∠FEO=∠ODA故tan∠FEO=tan∠ODA=![]() ,故③正确;当DA平分∠OAE时,OE=OD=1,设OF=a,延长AE至点H,则OH=DF=
,故③正确;当DA平分∠OAE时,OE=OD=1,设OF=a,延长AE至点H,则OH=DF=![]() ,在Rt△HOA中,HO=1+
,在Rt△HOA中,HO=1+![]() ,OA=3,HA=3+a,HO2+OA2=HA2 解得a=
,OA=3,HA=3+a,HO2+OA2=HA2 解得a=![]() ,故CG=2a=
,故CG=2a=![]() ,所以④正确.
,所以④正确.
详解:令x=0,得y=1,得OD=1,由OD=1得CD=2,易证△GCD∽△FOD,
∴S△GCD:S△FOD=4:1,故①错误;
在Rt△AOE中,AD>AE,所以AE的最大值为AD的长,AD=![]() ,故②正确;
,故②正确;
∵OD⊥OA,AE⊥DE
∴A、O、D、E四点共圆,
∵∠FEO+∠OEA=90°,∠ODA+∠OAD=90°,∠OEA=∠ODA(同弧所对的圆周角相等)
∴∠FEO=∠ODA
∴tan∠FEO=tan∠ODA=![]() ,故③正确;
,故③正确;
当DA平分∠OAE时,OE=OD=1
设OF=a,延长AE至点H,则OH=DF=![]()
在Rt△HOA中,HO=1+![]() ,OA=3,HA=3+a
,OA=3,HA=3+a
HO2+OA2=HA2 解得a=![]()
∴CG=2a=![]() ,故④正确.
,故④正确.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示的是用火柴棒搭成的一个个图形,第1个图形用了5根火柴,第2个图形用了8根火柴,![]() ,照此规律,用288根火柴搭成的图形是( ).
,照此规律,用288根火柴搭成的图形是( ).

A. 第80个图形B. 第82个图形
C. 第72个图形D. 第95个图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某小区开展了“节约用水为环保做贡献”的活动,为了解居民用水情况,在小区随机抽查了10户家庭的月用水量,结果如下表
月用水量(吨) | 8 | 9 | 10 |
户数 | 2 | 6 | 2 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A. 方差是4 B. 极差2 C. 平均数是9 D. 众数是9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为![]() ,点B坐标为
,点B坐标为![]() 满足
满足![]() .
.
(1)若![]() 没有平方根,判断点A在第几象限并说明理由;
没有平方根,判断点A在第几象限并说明理由;
(2)若点A到![]() 轴的距离是点B到
轴的距离是点B到![]() 轴距离的3倍,求点B的坐标;
轴距离的3倍,求点B的坐标;
(3)点D的坐标为(4,-2),△OAB的面积是△DAB面积的2倍,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布直方图(如图),请你根据图表提供的信息,解答下列问题:
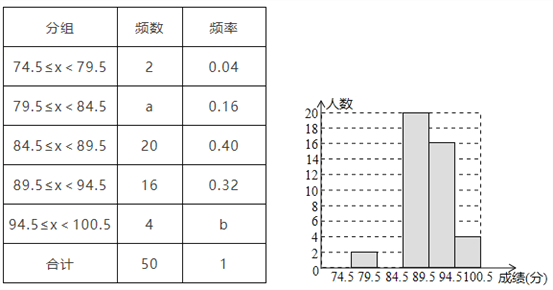
(1)频数、频率分布表中a=_______,b=_______;
(2)补全频数分布直方图;
(3)初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为![]() 其中
其中![]() .
.
![]() 四边形ABCD的是______
四边形ABCD的是______![]() 填写四边形ABCD的形状
填写四边形ABCD的形状![]()
![]() 当点A的坐标为
当点A的坐标为![]() 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值.
![]() 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
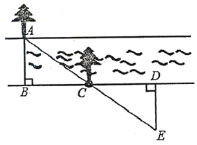
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一侧岸边B点,选对岸正对的一棵树A;
②沿河岸直走20米有一树C,继续前行20米到达D处;
③从D处沿与河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求河流的宽度是多少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
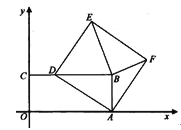
【题目】如图,在平面直角坐标系xoy中,矩形OABC的顶点B坐标为(12,5),点D在 CB边上从点C运动到点B,以AD为边作正方形ADEF,连BE、BF,在点D运动过程中,请探究以下问题:
(1)△ABF的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若△BEF为等腰三角形,求此时正方形ADEF的边长;
(3)设E(x,y),直接写出y关于x的函数关系式及自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com