
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为![]() 其中
其中![]() .
.
![]() 四边形ABCD的是______
四边形ABCD的是______![]() 填写四边形ABCD的形状
填写四边形ABCD的形状![]()
![]() 当点A的坐标为
当点A的坐标为![]() 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值.
![]() 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.

【答案】(1)平行四边形;(2)![]() ,
,![]() ,(3)四边形ABCD不可能成为菱形,理由见解析.
,(3)四边形ABCD不可能成为菱形,理由见解析.
【解析】
(1)根据正、反比例函数的对称性即可得出点A、C关于原点O成中心对称,再结合点B与点D关于坐标原点O成中心对称,即可得出对角线BD、AC互相平分,由此即可证出四边形ABCD的是平行四边形;
(2)由点A的纵坐标结合反比例函数图象上点的坐标特征即可求出n值,进而得出点A的坐标以及OA的长度,再根据矩形的性质即可得出OB=OA,由点B的坐标即可求出m值;
(3)由点A在第一象限内,点B在x轴正半轴上,可得出∠AOB<90°,而菱形的对角线互相垂直平分,由此即可得知四边形ABCD不可能成为菱形.
![]() 正比例函数
正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于A、C两点,
的图象分别交于A、C两点,
![]() 点A、C关于原点O成中心对称,
点A、C关于原点O成中心对称,
![]() 点B与点D关于坐标原点O成中心对称,
点B与点D关于坐标原点O成中心对称,
![]() 对角线BD、AC互相平分,
对角线BD、AC互相平分,
![]() 四边形ABCD的是平行四边形,
四边形ABCD的是平行四边形,
故答案为:平行四边形.
![]() 点
点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
![]() ,解得:
,解得:![]() ,
,
![]() 点
点![]() ,
,
![]() ,
,
![]() 四边形ABCD为矩形,
四边形ABCD为矩形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
![]() 四边形ABCD不可能成为菱形,理由如下:
四边形ABCD不可能成为菱形,理由如下:
![]() 点A在第一象限内,点B在x轴正半轴上,
点A在第一象限内,点B在x轴正半轴上,
![]() ,
,
![]() 与BD不可能互相垂直,
与BD不可能互相垂直,
![]() 四边形ABCD不可能成为菱形.
四边形ABCD不可能成为菱形.


科目:初中数学 来源: 题型:
【题目】如图,已知∠B=∠C.
(1)若AD∥BC,则AD平分∠EAC吗?请说明理由.
(2)若∠B+∠C+∠BAC=180°,AD平分∠EAC,则AD∥BC吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41.
≈1.41.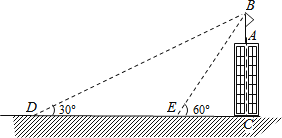
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )

A. AB//DC,AD//BC B. AB//DC,AD=BC
C. AO=CO,BO=DO D. AB=DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·![]() )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,DF是
,DF是![]() 的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG.
的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG.
![]() 求证:
求证:![]() ≌
≌![]() .
.
![]() 若
若![]() .
.
![]() 求CG的长.
求CG的长.
![]() 在
在![]() 的边上取一点P,在矩形DEFG的边上取一点Q,若以P,Q,C,G为顶点的四边形是平行四边形,求出所有满足条件的平行四边形的面积.
的边上取一点P,在矩形DEFG的边上取一点Q,若以P,Q,C,G为顶点的四边形是平行四边形,求出所有满足条件的平行四边形的面积.
![]() 在
在![]() 内取一点O,使四边形AOHD是平行四边形,连结OA,OB,OC,直接写出
内取一点O,使四边形AOHD是平行四边形,连结OA,OB,OC,直接写出![]() ,
,![]() ,
,![]() 的面积之比.
的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,第三行有4个点,第四行有8个点,….那么这个三角点阵中前n行的点数之和可能是( )

A. 510 B. 511 C. 512 D. 513
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,求∠FEB的度数.
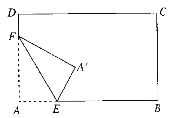
(2)如图,A地和B地都是海上观测站,从A地发现它的北偏东60方向有一艘船P,同时,从B地发现这艘船P在它北偏东30方向.试在图中画出这艘船P的位置.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com