Question

【题目】如图，在矩形ABCD中，AB=5，BC=3，点E为射线BC上一动点，将△ABE沿AE折叠，得到△AB′E．若B′恰好落在射线CD上，则BE的长为 ．

Answer 1

【答案】 或15
【解析】解：如图1，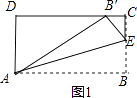
∵将△ABE沿AE折叠，得到△AB′E，
∴AB′=AB=5，B′E=BE，∴CE=3﹣BE，∵AD=3，∴DB′=4，∴B′C=1，∵B′E2=CE2+B′C2 ，
∴BE2=（3﹣BE）2+12 ，
∴BE= ，
如图2，

∵将△ABE沿AE折叠，得到△AB′E，
∴AB′=AB=5，
∵CD∥AB，
∴∠1=∠3，
∵∠1=∠2，
∴∠2=∠3，
∵AE垂直平分BB′，
∴AB=BF=5，
∴CF=4，
∵CF∥AB，
∴△CEF∽△ABE，
∴ ，
即 = ，
∴CE=12，∴BE=15，
综上所述：BE的长为： 或15，
所以答案是： 或15．
【考点精析】掌握矩形的性质和翻折变换（折叠问题）是解答本题的根本，需要知道矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．