
如图,P1是反比例函数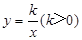 在第一象限图象上的一点,已知△P1O
A1为等边三角形,点A1 的坐标为(2,0).
在第一象限图象上的一点,已知△P1O
A1为等边三角形,点A1 的坐标为(2,0).

(1)直接写出点P1的坐标;
(2)求此反比例函数的解析式;
(3)若△P2A1A2为等边三角形,求点A2的坐标.
(1)P1(1, );(2)
);(2) ;(3)(
;(3)( ,0).
,0).
【解析】
试题分析:(1)由于△P1OA1为等边三角形,作P1C⊥OA1,垂足为C,由等边三角形的性质及勾股定理可求出点P1的坐标;
(2)根据点P1是反比例函数y= (k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式;
(k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式;
(3)作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
试题解析:(1)P1(1, );
);
(2)∵P1在反比例函数 (
( >0)图象上,∴
>0)图象上,∴ ,
,
∴ ,
,
∴反比例函数的解析式为 ;
;
(3)设等边三角形P2 A1 A2的边长为a(a>0),则A2(2+a,0).
如图,过P2作P2H⊥x轴,垂足为点H.

∴A1H= a,P2H=
P2 A1sin∠P2A1H=a·sin600=
a,P2H=
P2 A1sin∠P2A1H=a·sin600= ,
,
∴P2(2+ a,
a, ).
).
∵ P2在反比例函数 图象上,∴
图象上,∴ =
= ,
,
即 ,解得:
,解得: ,
, (舍去)
(舍去)
∴2+a= ,∴A2(
,∴A2( ,0)
,0)
考点: 反比例函数综合题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源:甘肃省中考真题 题型:解答题
 在第一象限图像上的一点,点A1的坐标为(2,0)。
在第一象限图像上的一点,点A1的坐标为(2,0)。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,P1是反比例函数![]() 在第一象限图像上的一点,点A1 的坐标为(2,0). (1)当点P1的横坐标逐渐增大时,△P1O A1的面积 将如何变化?
在第一象限图像上的一点,点A1 的坐标为(2,0). (1)当点P1的横坐标逐渐增大时,△P1O A1的面积 将如何变化?
(2)若△P1O A1与△P2 A1 A2均为等边三角形,求
此反比例函数的解析式及A2点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
 在第一象限图像上的一点,点A1的坐标为(2,0).
在第一象限图像上的一点,点A1的坐标为(2,0).
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:选择题
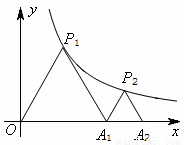
如图,P1是反比例函数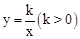 在第一象限图像上的一点,点A1 的坐标为(2,0).若△P1O A1与△P2 A1 A2均为等边三角形,则A2点的横坐标为
在第一象限图像上的一点,点A1 的坐标为(2,0).若△P1O A1与△P2 A1 A2均为等边三角形,则A2点的横坐标为
A.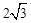 B.
B.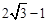 C.
C.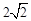 D.
D.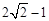
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com