
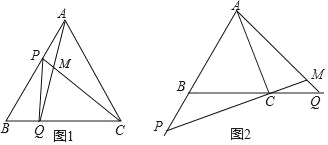
����Ŀ����ͼ1����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱ���ABC��AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s��
��1������AQ��CP���ڵ�M������P��Q�˶��Ĺ����У���CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ�����
��2�������ʱ��PBQ��ֱ�������Σ�
��3����ͼ2������P��Q���˶����յ�����������AB��BC���˶���ֱ��AQ��CP����ΪM������CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ�����
���𰸡���1����P��Q�˶��Ĺ����У���CMQ���䣬��CMQ=60�㣻��2����tΪ![]() s��
s��![]() s ʱ����PBQΪֱ�������Σ���3����P��Q�˶��Ĺ����У���CMQ�Ĵ�С���䣬��CMQ=120�㣮
s ʱ����PBQΪֱ�������Σ���3����P��Q�˶��Ĺ����У���CMQ�Ĵ�С���䣬��CMQ=120�㣮
�������������������1�����õȱ������ε����ʿ�֤����APC�ա�BQA�������á�BAQ=��ACP����������������ǵ����ʿ�֤�á�CMQ=60�㣻
��2������t�ֱ��ʾ��BP��BQ���֡�BPQ=90��͡�BPQ=90������������ֱ�����ֱ�������ε����ʿɵõ�����t�ķ��̣�������t��ֵ��
��3��ͬ��1����֤�á�PBC�ա�QCA����������������ǵ����ʿ���á�CMQ=120�㣮
�����������1���ߡ�ABCΪ�ȱ������Σ�
��AB=AC����B=��PAC=60�㣬
�ߵ�P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s��
��AP=BQ��
�ڡ�APC�͡�BQA��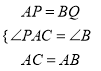 ��
��
���APC�ա�BQA��SAS����
���BAQ=��ACP��
���CMQ=��CAQ+��ACP=��BAQ+��CAQ=��BAC=60�㣬
����P��Q�˶��Ĺ����У���CMQ���䣬��CMQ=60�㣻
��2�����˶�ʱ��Ϊts����AP=BQ=t��
��PB=4��t��
����PQB=90��ʱ��
�ߡ�B=60�㣬
��PB=2BQ��
��4��t=2t�����t=![]() ��
��
����BPQ=90��ʱ��
�ߡ�B=60�㣬
��BQ=2PB��
��t=2��4��t�������t=![]() ��
��
�൱tΪ![]() s��
s��![]() s ʱ����PBQΪֱ�������Σ�
s ʱ����PBQΪֱ�������Σ�
��3���ڵȱ�������ABC�У�AC=BC����ABC=��BCA=60�㣬
���PBC=��QCA=120������BP=CQ��
�ڡ�PBC�͡�QCA��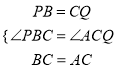 ��
��
���PBC�ա�QCA��SAS����
���BPC=��MQC��
�֡ߡ�PCB=��MCQ��
���CMQ=��PBC=120�㣬
����P��Q�˶��Ĺ����У���CMQ�Ĵ�С���䣬��CMQ=120�㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
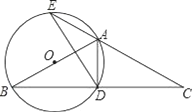
����Ŀ����ͼ����ABC�У�AB=AC����ABΪֱ������O����BC�ڵ�D����CA���ӳ����ڵ�E������AD��DE��
��1����֤��D��BC���е㣻
��2����DE=3��BD��AD=2�����O�İ뾶��
��3���ڣ�2���������£�����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У�����ȷ���ǣ� ��
A.8����������2
B.��8���������ǩ�2
C.0����������0
D.125���������ǡ�5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�����һ�κ���y=2x��3��ͼ���ϵ��ǣ�������
A. �� 2��3�� B. ��2��1�� C. ��0��3�� D. ��3��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ʽx2��mx+9��һ����ȫƽ��ʽ����ôm��ֵΪ�� ��
A.��3
B.��6
C.��3
D.��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A�ڵ������ޣ�������x��ľ������2����y��ľ������3�����A������Ϊ��������
A. ��3����2�� B. ��3��2�� C. ��2����3�� D. ��2��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��С��������ҵ�������ڼ乺��100ֻ�����ͺŵ��ľ߽������ۣ�����ۺ��ۼ�֮��Ĺ�ϵ���±���
�ͺ� | ���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� |
A�� | 10 | 12 |
B�� | 15 | 23 |
Ҫʹ�����ľ����������������۸��40%��������Ҫ��������ֻA���ľߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com