
【题目】菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.
(1)如图1,求∠BGD的度数;
(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;
(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=4![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.

【答案】(1)∠BGD=120°;(2)见解析;(3)S四边形ABCD=26![]() .
.
【解析】
(1)只要证明△DAE≌△BDF,推出∠ADE=∠DBF,由∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,推出∠BGD=180°-∠BGE=120°;
(2)如图3中,延长GE到M,使得GM=GB,连接BD、CG.由△MBD≌△GBC,推出DM=GC,∠M=∠CGB=60°,由CH⊥BG,推出∠GCH=30°,推出CG=2GH,由CG=DM=DG+GM=DG+GB,即可证明2GH=DG+GB;
(3)解直角三角形求出BC即可解决问题;
(1)解:如图1﹣1中,
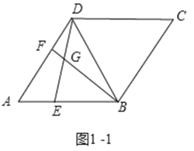
∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD是等边三角形,
∴AB=DB,∠A=∠FDB=60°,
在△DAE和△BDF中,
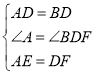 ,
,
∴△DAE≌△BDF,
∴∠ADE=∠DBF,
∵∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,
∴∠BGD=180°﹣∠BGE=120°.
(2)证明:如图1﹣2中,延长GE到M,使得GM=GB,连接CG.
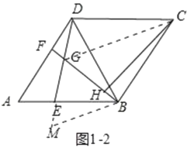
∵∠MGB=60°,GM=GB,
∴△GMB是等边三角形,
∴∠MBG=∠DBC=60°,
∴∠MBD=∠GBC,
在△MBD和△GBC中,
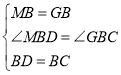 ,
,
∴△MBD≌△GBC,
∴DM=GC,∠M=∠CGB=60°,
∵CH⊥BG,
∴∠GCH=30°,
∴CG=2GH,
∵CG=DM=DG+GM=DG+GB,
∴2GH=DG+GB.
(3)如图1﹣2中,由(2)可知,在Rt△CGH中,CH=4![]() ,∠GCH=30°,
,∠GCH=30°,
∴tan30°=![]() ,
,
∴GH=4,
∵BG=6,
∴BH=2,
在Rt△BCH中,BC=![]() ,
,
∵△ABD,△BDC都是等边三角形,
∴S四边形ABCD=2S△BCD=2×![]() ×(
×(![]() )2=26
)2=26![]() .
.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
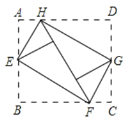
【题目】如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品共1200件,这两种商品的进价,售价如下表:
进价(元/件) | 售价(元/件) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)超市如何进货,进货款恰好为46000元;
(2)为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为20%,请问乙商品需打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.

(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
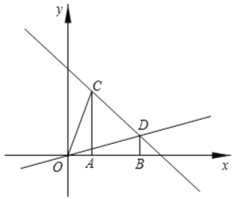
【题目】在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.
(1)求直线CD和直线OD的解析式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为![]() t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
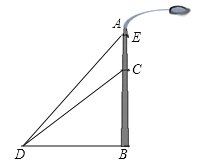
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)若n=8时,则S的值为_____________.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=__________________.
(3)根据上题的规律计算2+4+6+8+10+…+98+100![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() ,二次函数
,二次函数![]() 的图像经过点
的图像经过点![]() 、
、![]() ,且
,且![]() 满足
满足![]() (
(![]() 为常数).
为常数).
(1)若一次函数![]() 的图像经过
的图像经过![]() 、
、![]() 两点.
两点.
①当![]() 、
、![]() 时,求
时,求![]() 的值;
的值;
②若![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围.
的取值范围.
(2)当![]() 且
且![]() 、
、![]() 时,判断直线
时,判断直线![]() 与
与![]() 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(3)点![]() 、
、![]() 的位置随着
的位置随着![]() 的变化而变化,设点
的变化而变化,设点![]() 、
、![]() 运动的路线与
运动的路线与![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,线段
,线段![]() 的长度会发生变化吗?如果不变,求出
的长度会发生变化吗?如果不变,求出![]() 的长;如果变化,请说明理由.
的长;如果变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com