练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某超市计划购进甲、乙两种商品共1200件，这两种商品的进价，售价如下表：

    进价（元/件）

    售价（元/件）

    甲

    25

    30

    乙

    45

    60

    （1）超市如何进货，进货款恰好为46000元；

    （2）为确保乙商品畅销，在（1）的条件下，商家决定对乙商品进行打折出售，且全部售完后，乙商品的利润率为20%，请问乙商品需打几折？

    【答案】（1）故进货甲商品400件，乙商品800件；（2）则乙商品需打九折.

    【解析】

    （1）设甲种商品进货x件，则乙种商品进货（1200-x）件，再根据已知条件即可列出方程，再求出x即可；

    （2）设乙商品打y折，根据利润率为20%可列出方程，再解之即可.

    （1）设甲种商品进货x件，则乙种商品进货（1200-x）件，

    由题意得25x+45(1200-x)=46000,

    解得x=400，

    故进货甲商品400件，乙商品800件；

    （2）设乙商品打y折，

    由题意得

    解得y=9，

    则乙商品需打9折.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下面为某年11月的日历：

    日

    一

    二

    三

    四

    五

    六

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    (1)在日历上任意圈出一个竖列上相邻的3个数；

    ①设中间的一个数为，则另外的两个数为 、 ；

    ②若已知这三个数的和为42，则这三天都在星期 ；

    (2)在日历上用一个小正方形任意圈出其中的9个数，设圈出的9个数的中心的数为b,若这9个数的和为153，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

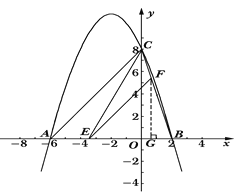
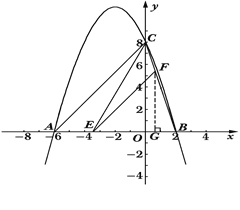
    【题目】已知：二次函数的图象与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2－10x＋16＝0的两个根，且A点坐标为（－6，0）．

    （1）求此二次函数的表达式；

    （2）若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

    【答案】（1）y＝－x2－x＋8（2）

    【解析】试题分析:(1)求出一元二次方程的两根即可求出两点坐标,把B、C两点坐标代入二次函数的解析式就可解答；

    (2)过点F作FG⊥AB，垂足为G，由EF∥AC，得△BEF∽△BAC，利用相似比求EF，利用sin∠FEG=sin∠CAB求FG，根据S=S△BCE-S△BFE，求S与m之间的函数关系式.

    解:(1）解方程x2－10x＋16＝0得x1＝2，x2＝8

    ∴B（2，0）、C（0，8）

    ∴所求二次函数的表达式为y＝－x2－x＋8

    （2）∵AB＝8，OC＝8，依题意，AE＝m，则BE＝8－m，

    ∵OA＝6，OC＝8， ∴AC＝10.

    ∵EF∥AC, ∴△BEF∽△BAC.

    ∴＝.　　即＝. ∴EF＝.

    过点F作FG⊥AB，垂足为G，

    则sin∠FEG＝sin∠CAB＝.∴＝.　

    ∴FG＝·＝8－m.

    ∴S＝S△BCE－S△BFE

    ＝

    （0＜m＜8）

    点睛:本题考查了一元二次方程的解法，待定系数法求函数关系系，相似三角形的判定与性质,span>锐角三角函数的定义，割补法求图形的面积，熟练掌握待定系数法求二次函数关系式、相似三角形的判定与性质是解答本题的关键.

    【题型】解答题
    【结束】
    23

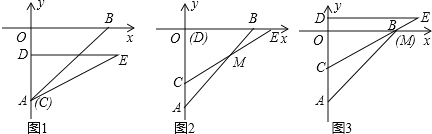
    【题目】如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．Rt△CDE中，∠CDE=90°，CD=4，DE=4，直角边CD在y轴上，且点C与点A重合．Rt△CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：

    （1）如图（2），当Rt△CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME的度数．

    （2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．

    （3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校计划在总费用元的限额内，租用汽车送名学生和名教师集体参加校外实践活动，为确保安全，每辆汽车上至少要有名教师．现有甲、乙两种大客车，它们的载客量和租金如下表所示．

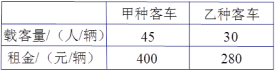
    （1）根据题干所提供的信息，确定共需租用多少辆汽车？

    （2）请你给学校选择一种最节省费用的租车方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某景区的水上乐园有一批人座的自划船，每艘可供至位游客乘坐游湖，因景区加大宣传，预计今年游客将会增加．水上乐园的工作人员在去年月日一天出租的艘次人自划船中随机抽取了艘，对其中抽取的每艘船的乘坐人数进行统计，并制成如下统计图.

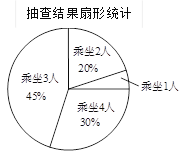
    （1）求扇形统计图中， “乘坐1人”所对应的圆心角度数；

    （2）估计去年月日这天出租的艘次人自划船平均每艘船的乘坐人数；

    （3）据旅游局预报今年月日这天该景区可能将增加游客300人，请你为景区预计这天需安排多少艘4人座的自划船才能满足需求．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

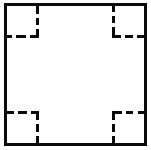
    【题目】如图，把一边长为厘米的正方形纸板的四个角各剪去一个边长为厘米的小正方形，然后把它折成一个无盖纸盒.

    （1）该纸盒的高是 厘米，底面积是 平方厘米；

    （2）该纸盒的全面积（外表面积）为 平方厘米；

    （3）为了使纸盒底面更加牢固且达到废物利用的目的，现考虑将剪下的四个小正方形平铺在盒子的底面，要求既不重叠又恰好铺满（不考虑纸板的厚度），求此时与之间的倍数关系.（直接写出答案即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

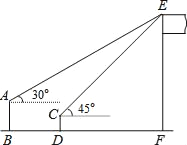
    【题目】如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．

    （1）求小敏到旗杆的距离DF．（结果保留根号）

    （2）求旗杆EF的高度．（结果保留整数，参考数据：≈1.4，≈1.7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】菱形ABCD中，∠BAD＝60°，BD是对角线，点E、F分别是边AB、AD上两个点，且满足AE＝DF，连接BF与DE相交于点G．

    （1）如图1，求∠BGD的度数；

    （2）如图2，作CH⊥BG于H点，求证：2GH＝GB+DG；

    （3）在满足（2）的条件下，且点H在菱形内部，若GB＝6，CH＝4，求菱形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下面三行单项式：

    x，2x2，4x3，8x4，16x5，32x6，…；①

    ﹣2x，4x2，﹣8x3，16x4，﹣32x5，64x6，…；②

    2x2，﹣3x3，5x4，﹣9x5，17x6，﹣33x7，…；③

    根据你发现的规律，解答下列问题

    （1）第①行的第8个单项式为　 　；

    （2）第②行的第9个单项式为　 　；第③行的第10个单项式为　 　；

    （3）取每行的第9个单项式，令这三个单项式的和为A．当x＝时，求512（A+）的值．

    查看答案和解析>>

    同步练习册答案