
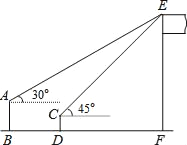
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
【答案】(1)DF=(4+3![]() )米;(2)旗杆的高度约为10米.
)米;(2)旗杆的高度约为10米.
【解析】试题分析:过点A作AM⊥EF于M,过点C作CN⊥EF于N,设CN=x,则EN=x,AM=5+x,可求EM,在RtΔAEM中利用三角函数关系可求出DF的长.
(2)由EM+FM可求出EF的长.
试题解析:(1)过点A作AM⊥EF于点M,过点C作CN⊥EF于点N.设CN= x
在RtΔECN中, ∵∠ECN=45°
∴EN=CN=x
∴EM=x+0.7-1.7=x-1
∵BD=5
∴AM=BF=5+x
在RtΔAEM中, ∵∠EAM=30°
∴![]()
∴![]()
解得![]()
即DF= 4+![]() (米)
(米)
(2)EF=x +0.7="4+"![]() +0.7=4+3×1.7+0.7=9.8≈10(米)
+0.7=4+3×1.7+0.7=9.8≈10(米)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:若数轴上![]() 两点分别对应实数
两点分别对应实数![]() ,则
,则![]() 两点之间的距离记作
两点之间的距离记作![]() ,且
,且![]() .已知点
.已知点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() 、点
、点![]() 在数轴上对应数字
在数轴上对应数字![]() .根据信息完成下列各题:
.根据信息完成下列各题:
(1)![]() =_____________.
=_____________.
(2)若数轴上点![]() 对应实数
对应实数![]() ,则
,则
①当![]() 时
时![]() =_____________;
=_____________;
②当![]() 取最小值时,
取最小值时,![]() 的取值范围为_____________.
的取值范围为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品共1200件,这两种商品的进价,售价如下表:
进价(元/件) | 售价(元/件) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)超市如何进货,进货款恰好为46000元;
(2)为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为20%,请问乙商品需打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是______事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每6个人中会有1人抽中一等奖、2人抽中二等奖,若袋中共有18个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中增加3个黄球,那么抽中一等奖的概率会怎样变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.

(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
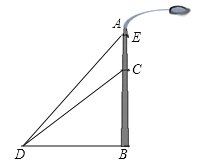
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如下三种不完整的统计图表.
组别 | 获取新闻的最主要途径 | 人数 |
| 电脑上网 | 280 |
| 手机上网 |
|
| 电视 | 140 |
| 报纸 |
|
| 其他 | 80 |
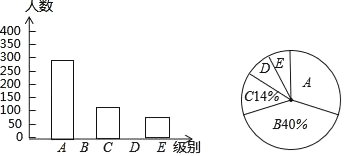
请根据图表信息解答下列问题:
(1)统计表中的![]() ,
,![]() ,并请补全条形统计图;
,并请补全条形统计图;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是 ;
”所对应的圆心角的度数是 ;
(3)若该市约有100万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com