练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一次函数 的图象与 、 轴分别交于点 、 ，直线 经过 上的三分之一点 ，且交 轴的负半轴于点 ，如果 ，求直线 的解析式．

    【答案】（1） 点的坐标为 或 （2） 或 ．

    【解析】试题分析: 根据y＝与y轴,x轴的交点分别为A,B,得出A,B两点的坐标,再根据D为OA上的三分之一点,得出D点的坐标,进而得出C点的坐标,即可求出解析式．

    试题解析:因为直线y＝与y轴,x轴的交点分别为A,B,所以两点坐标分别为A（0,3）,B（2,0）,所以OA=3,OB=2,所以S△AOB＝OAOB＝3,

    因为D为OA上的三分之一点,所以D点的坐标为（0,1）或（0,2）,

    因为S△AOB＝S△DOC＝OCOD＝3,所以当OD=1时,OC=6,当OD=2时,OC=3,

    因为点C在x轴的负半轴上,所以C点的坐标为（-6,0）或（-3,0）,

    所以直线CD的解析式为y＝或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有理数a，b，c在数轴上的位置如图所示，且|a|=|c|．

    （1）若|a+c|+|b|=2，求b的值；

    （2）用“＞”从大到小把a，b，﹣b，c连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为6，点E，F分别在AB，AD上，若CE＝3，且∠ECF＝45°，则CF的长为（ ）

    A. 2 B. 3 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

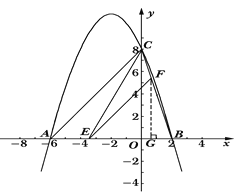
    【题目】已知：二次函数的图象与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2－10x＋16＝0的两个根，且A点坐标为（－6，0）．

    （1）求此二次函数的表达式；

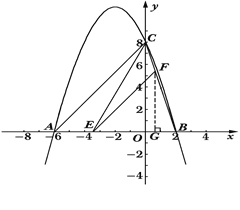
    （2）若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

    【答案】（1）y＝－x2－x＋8（2）

    【解析】试题分析:(1)求出一元二次方程的两根即可求出两点坐标,把B、C两点坐标代入二次函数的解析式就可解答；

    (2)过点F作FG⊥AB，垂足为G，由EF∥AC，得△BEF∽△BAC，利用相似比求EF，利用sin∠FEG=sin∠CAB求FG，根据S=S△BCE-S△BFE，求S与m之间的函数关系式.

    解:(1）解方程x2－10x＋16＝0得x1＝2，x2＝8

    ∴B（2，0）、C（0，8）

    ∴所求二次函数的表达式为y＝－x2－x＋8

    （2）∵AB＝8，OC＝8，依题意，AE＝m，则BE＝8－m，

    ∵OA＝6，OC＝8， ∴AC＝10.

    ∵EF∥AC, ∴△BEF∽△BAC.

    ∴＝.　　即＝. ∴EF＝.

    过点F作FG⊥AB，垂足为G，

    则sin∠FEG＝sin∠CAB＝.∴＝.　

    ∴FG＝·＝8－m.

    ∴S＝S△BCE－S△BFE

    ＝

    （0＜m＜8）

    点睛:本题考查了一元二次方程的解法，待定系数法求函数关系系，相似三角形的判定与性质,span>锐角三角函数的定义，割补法求图形的面积，熟练掌握待定系数法求二次函数关系式、相似三角形的判定与性质是解答本题的关键.

    【题型】解答题
    【结束】
    23

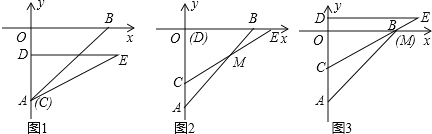
    【题目】如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．Rt△CDE中，∠CDE=90°，CD=4，DE=4，直角边CD在y轴上，且点C与点A重合．Rt△CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：

    （1）如图（2），当Rt△CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME的度数．

    （2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．

    （3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，是的边上的中线．

    （1）①用尺规完成作图：延长到点，使，连接；

    ② 若，求的取值范围；

    （2）如图2，当时，求证：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校计划在总费用元的限额内，租用汽车送名学生和名教师集体参加校外实践活动，为确保安全，每辆汽车上至少要有名教师．现有甲、乙两种大客车，它们的载客量和租金如下表所示．

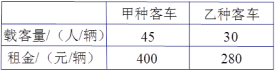
    （1）根据题干所提供的信息，确定共需租用多少辆汽车？

    （2）请你给学校选择一种最节省费用的租车方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某景区的水上乐园有一批人座的自划船，每艘可供至位游客乘坐游湖，因景区加大宣传，预计今年游客将会增加．水上乐园的工作人员在去年月日一天出租的艘次人自划船中随机抽取了艘，对其中抽取的每艘船的乘坐人数进行统计，并制成如下统计图.

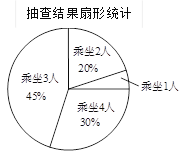
    （1）求扇形统计图中， “乘坐1人”所对应的圆心角度数；

    （2）估计去年月日这天出租的艘次人自划船平均每艘船的乘坐人数；

    （3）据旅游局预报今年月日这天该景区可能将增加游客300人，请你为景区预计这天需安排多少艘4人座的自划船才能满足需求．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

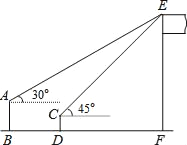
    【题目】如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．

    （1）求小敏到旗杆的距离DF．（结果保留根号）

    （2）求旗杆EF的高度．（结果保留整数，参考数据：≈1.4，≈1.7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

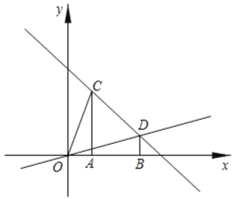
    【题目】在平面直角坐标系中，过点C（1，3）、D（3，1）分别作x轴的垂线，垂足分别为A、B．

    （1）求直线CD和直线OD的解析式；

    （2）点M为直线OD上的一个动点，过M作x轴的垂线交直线CD于点N，是否存在这样的点M，使得以A、C、M、N为顶点的四边形为平行四边形？若存在，求此时点M的横坐标；若不存在，请说明理由；

    （3）若△AOC沿CD方向平移（点C在线段CD上，且不与点D重合），在平移的过程中，设平移距离为t，△AOC与△OBD重叠部分的面积记为s，试求s与t的函数关系式．

    查看答案和解析>>

    同步练习册答案