
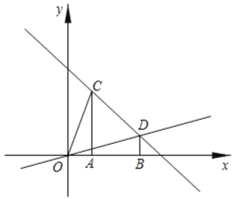
【题目】在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.
(1)求直线CD和直线OD的解析式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为![]() t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
【答案】(1)直线OD的解析式为y=![]() x;(2)存在.满足条件的点M的横坐标
x;(2)存在.满足条件的点M的横坐标![]() 或
或![]() ,理由见解析;(3)S=﹣
,理由见解析;(3)S=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
【解析】
(1)理由待定系数法即可解决问题;
(2)如图,设M(m,![]() m),则N(m,-m+4).当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,可得|-m+4-
m),则N(m,-m+4).当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,可得|-m+4-![]() m|=3,解方程即可;
m|=3,解方程即可;
(3)如图,设平移中的三角形为△A′O′C′,点C′在线段CD上.设O′C′与x轴交于点E,与直线OD交于点P;设A′C′与x轴交于点F,与直线OD交于点Q.根据S=S△OFQ-S△OEP=![]() OFFQ-
OFFQ-![]() OEPG计算即可;
OEPG计算即可;
(1)设直线CD的解析式为y=kx+b,则有![]() ,解得
,解得![]() ,
,
∴直线CD的解析式为y=﹣x+4.
设直线OD的解析式为y=mx,则有3m=1,m=![]() ,
,
∴直线OD的解析式为y=![]() x.
x.
(2)存在.
理由:如图,设M(m,![]() m),则N(m,﹣m+4).
m),则N(m,﹣m+4).
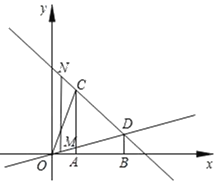
当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,
∴|﹣m+4﹣![]() m|=3,
m|=3,
解得m=![]() 或
或![]() ,
,
∴满足条件的点M的横坐标![]() 或
或![]() .
.
(3)如图,设平移中的三角形为△A′O′C′,点C′在线段CD上.
设O′C′与x轴交于点E,与直线OD交于点P;
设A′C′与x轴交于点F,与直线OD交于点Q.
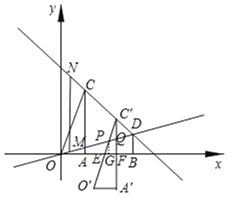
因为平移距离为![]() t,所以水平方向的平移距离为t(0≤t<2),
t,所以水平方向的平移距离为t(0≤t<2),
则图中AF=t,F(1+t,0),Q(1+t,![]() +
+![]() t),C′(1+t,3﹣t).
t),C′(1+t,3﹣t).
设直线O′C′的解析式为y=3x+b,
将C′(1+t,3﹣t)代入得:b=﹣4t,
∴直线O′C′的解析式为y=3x﹣4t.
∴E(![]() t,0).
t,0).
联立y=3x﹣4t与y=![]() x,解得x=
x,解得x=![]() t,
t,
∴P(![]() t,
t,![]() t).
t).
过点P作PG⊥x轴于点G,则PG=![]() t.
t.
∴S=S△OFQ﹣S△OEP=![]() OFFQ﹣
OFFQ﹣![]() OEPG
OEPG
=![]() (1+t)(
(1+t)(![]() +
+![]() t)﹣
t)﹣![]()
![]() t
t![]() t
t
=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.

(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
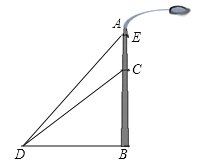
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知含字母a,b的代数式是:![]() .
.
(1)化简代数式;
(2)小红取a,b互为倒数的一对数值代入化简的代数式中,计算后得代数式的值等于0.那么小红所取的字母b的值等于多少?
(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取什么数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)若n=8时,则S的值为_____________.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=__________________.
(3)根据上题的规律计算2+4+6+8+10+…+98+100![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )

A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如下三种不完整的统计图表.
组别 | 获取新闻的最主要途径 | 人数 |
| 电脑上网 | 280 |
| 手机上网 |
|
| 电视 | 140 |
| 报纸 |
|
| 其他 | 80 |
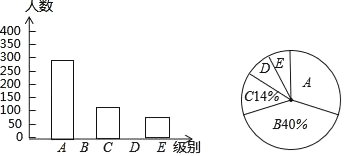
请根据图表信息解答下列问题:
(1)统计表中的![]() ,
,![]() ,并请补全条形统计图;
,并请补全条形统计图;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是 ;
”所对应的圆心角的度数是 ;
(3)若该市约有100万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
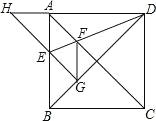
A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com