Question

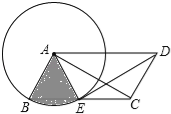
【题目】如图，ABCD中，AB=2，以点A为圆心，AB为半径的圆交边BC于点E，连接DE、AC、AE．

（1）求证：△AED≌△DCA；

（2）若DE平分∠ADC且与⊙A相切于点E，求图中阴影部分（扇形）的面积．

Answer 1

【答案】（1）见解析；（2）π．

【解析】试题分析：（1）由四边形ABCD是平行四边形，AB=AE，易证得四边形AECD是等腰梯形，即可得AC=DE，然后由SSS，即可证得：△AED≌△DCA；

（2）由DE平分∠ADC且与⊙A相切于点E，可求得∠EAD的度数，继而求得∠BAE的度数，然后由扇形的面积公式求得阴影部分（扇形）的面积．

（1）证明：∵四边形ABCD是平行四边形，

∴AB=CD，AD∥BC，

∴四边形AECD是梯形，

∵AB=AE，

∴AE=CD，

∴四边形AECD是等腰梯形，

∴AC=DE，

在△AED和△DCA中，

，

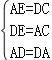∴△AED≌△DCA（SSS）；

（2）解：∵DE平分∠ADC，

∴∠ADC=2∠ADE，

∵四边形AECD是等腰梯形，

∴∠DAE=∠ADC=2∠ADE，

∵DE与⊙A相切于点E，

∴AE⊥DE，

即∠AED=90°，

∴∠ADE=30°，

∴∠DAE=60°，

∴∠DCE=∠AEC=180°﹣∠DAE=120°，

∵四边形ABCD是平行四边形，

∴∠BAD=∠DCE=120°，

∴∠BAE=∠BAD﹣∠EAD=60°，

∴S阴影=×π×22=π．