
����Ŀ����ͼ��ֱ��l��y=��x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮
��1�����AOB���ܳ���
��2����AQ=t��0�����ú�t�Ĵ���ʽ��ʾ��P�����ꣻ
��3��������P��Q��ֱ��l���˶���ʹ�á�AOQ���BPO���ܳ����ʱ����tan��AOQ=m��������A�Ķ��κ���y=ax2+bx+cͬʱ������������������
��6a+3b+2c=0��
�ڵ�m��x��m+2ʱ������y�����ֵ����![]() ���������ϵ��a��ֵ��
���������ϵ��a��ֵ��

���𰸡�(1) ��AOB�ܳ�Ϊ2+![]() ��(2) P����
��(2) P����![]() ��1+
��1+![]() ����(3) a��ֵΪ
����(3) a��ֵΪ![]() ��2
��2![]() ��2��
��2��
��������
�����������1�������A��B���꣬�����OB��OA��AB���ɽ�����⣮��2���ɡ�PBO�ס�OAQ����![]() =
=![]() �����PB���ٸ��ݵ���ֱ�����������ʿ�����õ�P���꣮��3�������m��ֵ���֢�a��0����a��0���������Σ����ö��κ������ʷֱ���⼴�ɣ�
�����PB���ٸ��ݵ���ֱ�����������ʿ�����õ�P���꣮��3�������m��ֵ���֢�a��0����a��0���������Σ����ö��κ������ʷֱ���⼴�ɣ�
�����������1���ں���y=��x+1�У���x=0����y=1��
��B��0��1����
��y=0����x=1��
��A��1��0����
��OA=OB=1��AB=![]() ��
��
���AOB�ܳ�Ϊ1+1+![]() =2+
=2+![]() ��
��
��2����OA=OB��
���ABO=��BAO=45�㣬
���PBO=��QAO=135�㣬
���POB=x�����OPB=��AOQ=135�㩁x��90��=45�㩁x��
���PBO�ס�OAQ��
��![]() =
=![]() ��
��
��PB=![]() =
=![]() ��
��
����P��PH��OB��H�㣬

���PHBΪ����ֱ�������Σ�
��PB=![]() ��
��
��PH=HB=![]() ��
��
��P����![]() ��1+
��1+![]() ����
����
��3���ɣ�2����֪��PBO�ס�OAQ�������ǵ��ܳ���ȣ������Ʊ�Ϊ1����ȫ�ȣ�
��PB=AQ��
��![]() =t��
=t��
��t��0��
��t=1��
ͬ���ɵ�Q��1+![]() ����
����![]() ����
����
��m=![]() =
=![]() ��1��
��1��
�������߾�����A��
��a+b+c=0��
�֡�6a+3b+2c=0��
��b=��4a��c=3a��
�Գ���x=2��ȡֵ��Χ![]() ��1��x
��1��x![]() +1��
+1��
����a��0�������ϣ�
������x=![]() ��1ʱȡ�����ֵ
��1ʱȡ�����ֵ![]() =2
=2![]() +2��
+2��
����![]() ��1��2a+��
��1��2a+��![]() ��1��b+c=2
��1��b+c=2![]() +2��
+2��
���a=![]() ��
��
����a��0�������£�
������x=2ʱȡ�����ֵ2![]() +2��
+2��
��4a+2b+c=2![]() +2��
+2��
���a=��2![]() ��2��
��2��
������������a��ֵΪ![]() ��2
��2![]() ��2��
��2��


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݣ�1����1��3��x��4������Ψһ��������4�����������ݵ���λ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г�����������ӳ���¼��У������Դ�С��С���ǣ�������
A.������
B.�������
C.���ն���
D.Ϧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ؼ�����ɵõ�ƽ��ͼ�Σ��ڱ�ʾ���������ĸ���������ɽس���ƽ��ͼ�εĺ���.
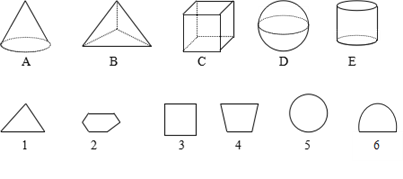
A�� ����B�� ����C�� ����D�� ����E�� ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ�����ܵƣ���֪1ֻA�ͽ��ܵƺ�3ֻB�ͽ��ܵƹ���26Ԫ��3ֻA�ͽ��ܵƺ�2ֻB�ͽ��ܵƹ���29Ԫ.
��1����һֻA�ͽ��ܵƺ�һֻB�ͽ��ܵƵ��ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵĽ��ܵƹ�50ֻ������A�ͽ��ܵƵ�����������B�ͽ��ܵ�������3��������Ƴ���ʡǮ�Ĺ�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�AB=2���Ե�AΪԲ�ģ�ABΪ�뾶��Բ����BC�ڵ�E������DE��AC��AE��

��1����֤����AED�ա�DCA��
��2����DEƽ����ADC������A�����ڵ�E����ͼ����Ӱ���֣����Σ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0������A����3��0����B��5��0����C��0��5�����㣬OΪ����ԭ��
��1����������ߵĽ���ʽ��
��2������������y=ax2+bx+c��a��0������ƽ��![]() ����λ���ȣ�������ƽ��n��n��0������λ���ȵõ��������ߣ����������ߵĶ���M�ڡ�ABC�ڣ���n��ȡֵ��Χ��
����λ���ȣ�������ƽ��n��n��0������λ���ȵõ��������ߣ����������ߵĶ���M�ڡ�ABC�ڣ���n��ȡֵ��Χ��
��3�����P��y���ϣ��������OPA+��OCA=��CBA����CP�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com