
某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
X(元) | 3 | 4 | 5 | 6 |
y(个) | 20 | 15 | 12 | 10 |
(1)根据表中的数据在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
科目:初中数学 来源: 题型:
已知四边形ABCD是平行四边形,对角线AC与BD相交于点O,那么下列结论中正确
的是
(A)当AB=BC时,四边形ABCD是矩形;
(B)当AC⊥BD时,四边形ABCD是矩形;
(C)当OA=OB时,四边形ABCD是矩形;
(D)当∠ABD=∠CBD时,四边形ABCD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
五一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加 ,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分)之间的关系如图所示.
,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分)之间的关系如图所示.
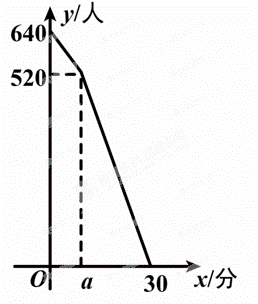
(1)求a的值.
(2)求检票到第20分钟时,候车室排队等候检票的旅客人数.
(3)若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问:检票一开始至少需要同时开放几个检票口?
查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x件.
(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y= (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y= (x>0)的图象相交于点F(p,q).
(x>0)的图象相交于点F(p,q).
(1)当F点恰好为线段的中点时,求直线AF的解析式 (用含a的代数式表示);
(2)若直线AF分别与x轴、y轴交于点M、N,当q=-a2+5a时,令S=S△ANO+S△MFO(其中O是原点),求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在该空地上种草皮,经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需200元,问:需要投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com