某工厂现有甲种原料380千克，乙种原料290千克，计划用这两种原料生产A、B两种产品共50件．已知生产一件A产品需要甲种原料9千克，乙种原料3千克，可获利700元；生产一件B产品需要甲种原料4千克，乙种原料10千克，可获利1200元．设生产A、B两种产品总利润为y元，其中A种产品生产件数是x件．
（1）写出y与x之间的函数关系式；
（2）如何安排A、B两种产品的生产件数，使总利润y有最大值，并求出y的最大值．
（1）y=﹣500x+60000；
（2）生产A种产品30件，B种产品20件，总利润y有最大值，y最大=45000元．
【解析】
试题分析：（1）根据等量关系“利润=A种产品的利润+B种产品的利润”可得出函数关系式；
（2）这是一道根据一次函数关系式的求最值问题，可根据等量关系：总利润=A种产品的利润+B种产品的利润，可得出函数关系式，然后根据题目中的两个不等关系“①生产A产品所需甲原料+生产B产品所需甲原料≤360，②生产A产品所需乙原料+生产B产品所需乙原料≤290”列出不等式组，解不等式组确定
自变量的取值范围，从而由函数y随x的变化求出最大利润．
试题解析：解：（1）y=700x+1200（50﹣x），
即y=﹣500x+60000；
（2）由题意得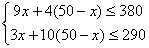
，
解得30≤x≤36
∵y=﹣500x+60000，
-500＜0，
∴y随x的增大而减小，
∴当x=30时，y最大=45000，
∴生产A种产品30件，B种产品20件，总利润y有最大值，y最大=45000元．
【难度】较难
快乐暑假暑假能力自测中西书局系列答案科目：初中数学 来源： 题型：
一张正方形的纸片，剪去两个一样的
小矩形得到一个“E”图案，如图所示，设小矩形的长和宽分别为x、y，剪去部分的面积为20，若2≤x≤10，则y与x的函数图象是（ ）
|
查看答案和解析>>
科目：初中数学 来源： 题型：
某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系：
X（元） | 3 | 4 | 5 | 6 |
y（个） | 20 | 15 | 12 | 10 |
（1）根据表中的数据在平面直角坐标系中描出实数对（x,y）的对应点．
（2）猜测并确定y与x之间的函数关系式，并画出图象；
（3）设经营此贺卡的销售利润为w元，试求出w与x之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过10元／个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？
查看答案和解析>>
科目：初中数学 来源： 题型：
“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的时间，y1表示乌龟所行的路程，y2表示兔子所行的路程）．有下列说法：
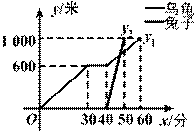
①“龟兔再次赛跑”的路程为1000米；
②兔子和乌龟同时从起点出发；
③乌龟在途中休息了10分钟；
④兔子比乌龟先到达终点．
其中正确的说法是________．（把你认为正确说法的序号都填上）
查看答案和解析>>
科目：初中数学 来源： 题型：
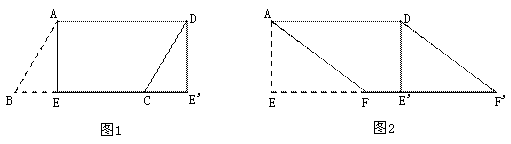
（1）如图1，纸片□ABCD中，AD=5，S□ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′ 的位置，拼成四边形AEE′D，则四边形AEE′D的形状为（ ）
A．平行四边形 B．菱形 C．矩形 D．正方形
（2）如图2，在（1）中的四边形纸片AEE′D中，在EE′上取一点F，使EF=4，剪下△AEF，将它平移至△DE′F′ 的位置，拼成四边形AFF′D．
① 求证四边形AFF′D是菱形；
② 求四边形AFF′D两条对角线的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
； （B）
； （C）
； （D）
．
是菱形，对角线
和
相交于点
，
，
，则这个菱形的面积是 
．
