
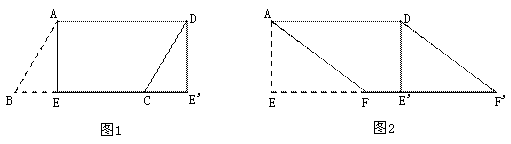
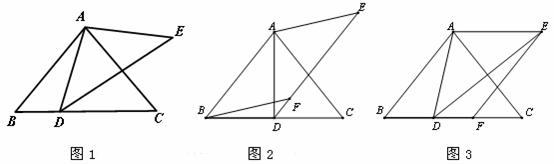
(1)如图1,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′ 的位置,拼成四边形AEE′D,则四边形AEE′D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
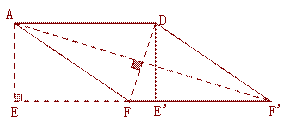
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′ 的位置,拼成四边形AFF′D.
① 求证四边形AFF′D是菱形;
② 求四边形AFF′D两条对角线的长.

(1)C;
(2)①由AF 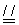 DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
②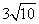 和
和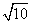 .
.
【解析】
试题分析:(1)由平移的性质得到AE 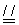 DE′,故四边形AEE′D是平行四边形,又AE⊥BC,得到∠AEE′=90°,所以四边形AEE′D是矩形,故C选项正确;
DE′,故四边形AEE′D是平行四边形,又AE⊥BC,得到∠AEE′=90°,所以四边形AEE′D是矩形,故C选项正确;
(2)①由AF 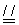 DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
DF′,得到四边形AFF′D是平行四边形,由AE=3,EF=4 ,∠E=90°,得到AF=5,而S□ABCD=AD·AE=15,所以AD=5, AD=AF,所以四边形AFF′D是菱形;
② 如图,连接AF′,DF ,在Rt△AEF′中,可以得到AF′=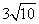 ,在Rt△DFE′中,可以得到DF=
,在Rt△DFE′中,可以得到DF=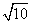 ,故四边形AFF′D两条对角线的长分别是
,故四边形AFF′D两条对角线的长分别是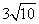 和
和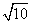 .
.
试题解析:(1)由平移知:AE DE′,∴四边形AEE′D是平行四边形,又AE⊥BC,∴∠AEE′=90°,∴四边形AEE′D是矩形,∴C选项正确;
DE′,∴四边形AEE′D是平行四边形,又AE⊥BC,∴∠AEE′=90°,∴四边形AEE′D是矩形,∴C选项正确;
(2)① ∵AF 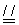 DF′,∴四边形AFF′D是平行四边形,∵AE=3,EF=4 ,∠E=90°,∴AF=5,∵AD=5 ,∴AD=AF , ∴四边形AFF′D是菱形;
DF′,∴四边形AFF′D是平行四边形,∵AE=3,EF=4 ,∠E=90°,∴AF=5,∵AD=5 ,∴AD=AF , ∴四边形AFF′D是菱形;
② 如下图,连接AF′,DF ,在Rt△AEF′中,AE=3,EF′=9, ∴AF′=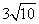 ,在Rt△DFE′中, FE′=1, DE′=AE=3, ∴DF=
,在Rt△DFE′中, FE′=1, DE′=AE=3, ∴DF=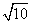 ,∴四边形AFF′D两条对角线的长分别是
,∴四边形AFF′D两条对角线的长分别是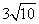 和
和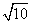 .
.

【难度】一般


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x件.
(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在该空地上种草皮,经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需200元,问:需要投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在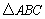 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =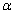 ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作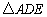 ,使AE=AD,
,使AE=AD,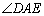 +
+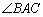 =180°.
=180°.
(1)直接写出∠ADE的度数(用含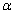 的式子表示);
的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com