
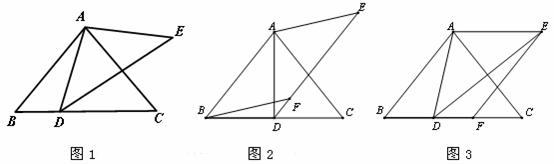
如图1,在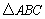 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =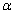 ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作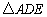 ,使AE=AD,
,使AE=AD,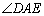 +
+ =180°.
=180°.
(1)直接写出∠ADE的度数(用含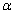 的式子表示);
的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
(1)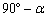
 (2)①证明:∵四边形ABFE是平行四边形,
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥E F.
F.
∴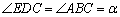 .
.
由(1)知,∠ADE = 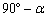 ,
,
∴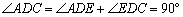 .
.
∴AD⊥BC.
∵AB=AC,
∴BD=CD.
②证明:
∵AB=AC,∠ABC =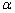 ,
,
∴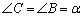 .
.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴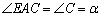 .
.
由(1)知,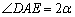 ,
,
∴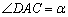 .
.
∴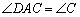 .
.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
【解析】
试题分析:(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°-2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
试题解析:(1)∠ADE = 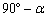 .
.
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥E F.
F.
∴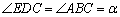 .
.
由(1)知,∠ADE = 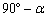 ,
,
∴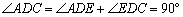 .
.
∴AD⊥BC.
∵AB=AC,
∴BD=CD.
②证明:
∵AB=AC,∠ABC =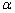 ,
,
∴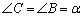 .
.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴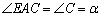 .
.
由(1)知,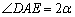 ,
,
∴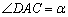 .
.
∴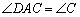 .
.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
【难度】较难


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
如图,已知在△ABC中,射线AM∥BC,P是边BC上一动点,∠APD=∠B,PD交射线AM于点D,联结CD.AB=4,BC=6,∠B=60°.
(1)求证: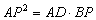 ;
;
(2)如果以AD为半径的圆A与以BP为半径的圆B相切,求线段BP的长度;
(3)将△ACD绕点A旋转,如果点 D恰好与点B重合,点C落在点E的位置上,求此时∠BEP的余切值.
D恰好与点B重合,点C落在点E的位置上,求此时∠BEP的余切值.

查看答案和解析>>
科目:初中数学 来源: 题型:
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
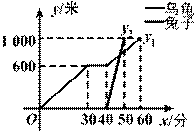

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子比乌龟先到达终点.
其中正确的说法是________.(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上,AE=2.
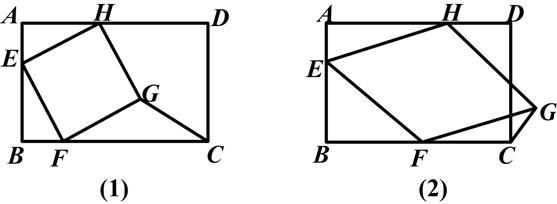
(1)如图(1),当四边形EFGH为正方形时,求△GFC的面积.
(2)如图(2),当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用含a的代数式表示).
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
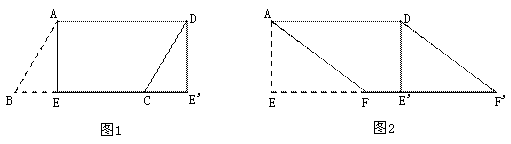
(1)如图1,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′ 的位置,拼成四边形AEE′D,则四边形AEE′D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′ 的位置,拼成四边形AFF′D.
① 求证四边形AFF′D是菱形;
② 求四边形AFF′D两条对角线的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
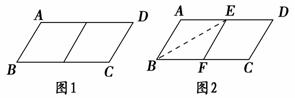
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作:在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依次类推,若第n次操作余下的 四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
(1)判断与推理:

①邻边长分别为2和3的平行四边形是________阶准菱形;
②小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(2)操作、探究与计算:
①已知▱ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出▱ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知▱ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出▱ABCD是几阶准菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com