
已知:如图,在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上,AE=2.
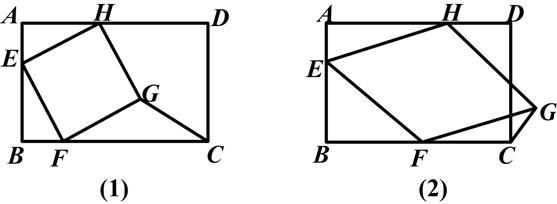
(1)如图(1),当四边形EFGH为正方形时,求△GFC的面积.
(2)如图(2),当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用含a的代数式表示).
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
(1)10 (2)12-a (3)不能
【解析】
解:(1)过点G作GM⊥BC于M.
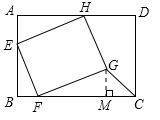
在正方形EFGH中,
∠HEF=90°,EH=EF,
∴∠AEH+∠BEF=90°.
∵∠AEH+∠AHE=90°,
∴∠AHE=∠BEF.
又∵∠A=∠B=90°,
∴△AHE≌△BEF.
同理可证△MFG≌△BEF.
∴GM=BF=AE=2.∴FC=BC-BF=10.
∴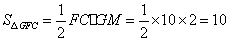 .
.
(2)过点G作GM⊥BC交BC的延长线于M,连接HF.
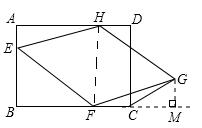
∵AD∥BC,∴∠AHF=∠MFH.
∵EH∥FG,∴∠EHF=∠GFH.
∴∠AHE=∠MFG.
又∵∠A=∠GMF=90°,EH=GF,
∴△AHE≌△MFG.∴GM=AE=2.
∴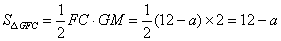 .
.
(3)△GFC的面积不能等于2.
说明:∵若S△GFC=2,则12-a=2,∴a=10.
此时,在△BEF中,
 .
.
在△AHE中,
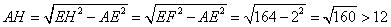 ,
,
∴AH>AD,即点H已经不在边AD上,故不可能有S△GFC=2.
【难度】困难


科目:初中数学 来源: 题型:
如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
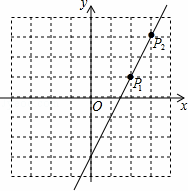

(1)写出点P2的坐标;
(2)求直线l所表示的一次函数的表达式;
(3)若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3.请判断点P3是否在直线l上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
某市实行中考改革,需要根据该市中学生体能的实际情况重新制定中考体育标准.为此,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试.测试的情况绘制成表格如下:

(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
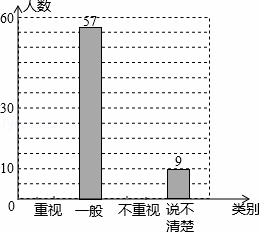
某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表
类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在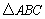 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =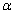 ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作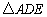 ,使AE=AD,
,使AE=AD,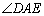 +
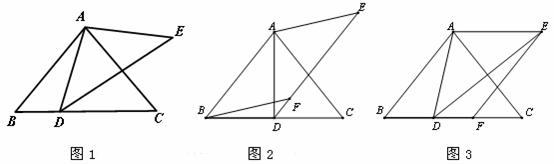
+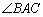 =180°.
=180°.
(1)直接写出∠ADE的度数(用含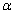 的式子表示);
的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,点E是边AD的中点,BE的延长线与CD的延长线相交于点F.
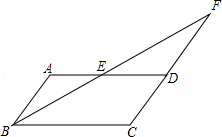
(1)求证:△ABE≌△DFE;
(2)试连接BD、AF,判断四边形ABDF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com