如图，在平行四边形ABCD中，点E是边AD的中点，BE的延长线与CD的延长线相交于点F．
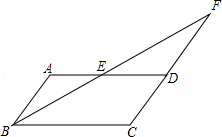
（1）求证：△ABE≌△DFE；
（2）试连接BD、AF，判断四边形ABDF的形状，并证明你的结论．
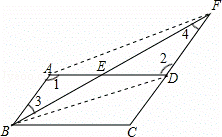
（1）证明：∵四边形ABCD是平行四边形，∴AB∥CF，∴∠1=∠2，∠3=∠4，
∵E是AD的中点，∴AE=DE，∴△ABE≌△DFE；
（2）四边形ABDF是平行四边形．理由如下：
∵△ABE≌△DFE，∴AB=DF，又∵AB∥DF，∴四边形ABDF是平行四边形．
【解析】
分析：（1）用ASA证明△ABE≌△DFE；
（2）四边形ABDF是平行四边形，可用对角线互相平分的四边形是平行四边形来证明．
解：（1）∵四边形ABCD是平行四边形，∴AB∥CF，∴∠1=∠2，∠3=∠4，
∵E是AD的中点，∴AE=DE，∴△ABE≌△DFE；
（2）四边形ABDF是平行四边形．理由如下：
∵△ABE≌△DFE，∴AB=DF，又∵AB∥DF，∴四边形ABDF是平行四边形．
【难度】一般
科目：初中数学 来源： 题型：
如图，在平面直角坐标系xOy中，已知正比例函数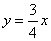
与一次函数
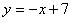的图像交于点A．
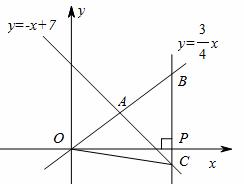
（1）求点A的坐标；
（2）设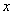
轴上一点P（
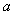，0），过点P作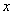轴的垂线（垂线位于点A的右侧），分别交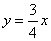和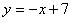的图像于点B、C，连接OC，若BC=
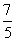OA,求△OBC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：如图，在矩形ABCD中，AB＝10，BC＝12，四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上，AE＝2．
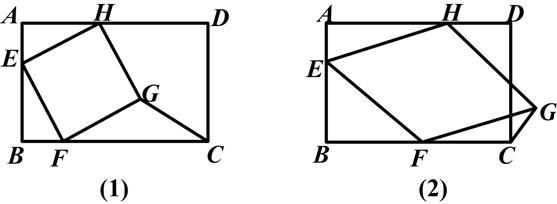
（1）如图（1），当四边形EFGH为正方形时，求△GFC的面积．
（2）如图（2），当四边形EFGH为菱形，且BF＝a时，求△GFC的面积（用含a的代数式表示）．
（3）在（2）的条件下，△GFC的面积能否等于2？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作：在余下的四边形纸片中再剪去一个菱形，又剩下一个四边形，称为第二次操作；…依次类推，若第n次操作余下的
四边形是菱形，则称原平行四边形为n阶准菱形．如图1，▱ABCD中，若AB＝1，BC＝2，则▱ABCD为1阶准菱形．
（1）判断与推理：
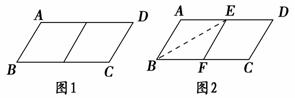
①邻边长分别为2和3的平行四边形是________阶准菱形；
②小明为了剪去一个菱形，进行了如下操作：如图2，把▱ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE．请证明四边形ABFE是菱形．
（2）操作、探究与计算：
①已知▱ABCD的邻边长分别为1，a（a＞1），且是3阶准菱形，请画出▱ABCD及裁剪线的示意图，并在图形下方写出a的值；
②已知▱ABCD的邻边长分别为a，b（a＞b），满足a＝6b＋r，b＝5r，请写出▱ABCD是几阶准菱形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图象在第二、四象限，那么
的取值范围是 . 
；
．