
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3),B(-3,2),C(-1,1).

(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点旋转180°后得到的△A2B2C2;
(3)△A'B'C'与△ABC是位似图形,请写出位似中心的坐标:______;
(4)顺次连接C,C1,C',C2,所得到的图形是轴对称图形吗?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:

下列说法正确的是( )
A. 抛物线的开口向下
B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2
D. 抛物线的对称轴是x=-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个圆形喷水池的中心竖立一根高为![]() 顶端装有喷头的水管,喷头喷出的水柱呈抛物线形.当水柱与池中心的水平距离为
顶端装有喷头的水管,喷头喷出的水柱呈抛物线形.当水柱与池中心的水平距离为![]() 时,水柱达到最高处,高度为
时,水柱达到最高处,高度为![]() .
.
![]() 求水柱落地处与池中心的距离;
求水柱落地处与池中心的距离;
![]() 如果要将水柱的最大高度再增加
如果要将水柱的最大高度再增加![]() ,水柱的最高处与池中心的水平距离以及落地处与池中心的距离仍保持不变,那么水管的高度应是多少?
,水柱的最高处与池中心的水平距离以及落地处与池中心的距离仍保持不变,那么水管的高度应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,经过原点
,经过原点![]() 且与
且与![]() 轴另一交点为
轴另一交点为![]() .
.
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 若
若![]() 为等腰直角三角形,求抛物线
为等腰直角三角形,求抛物线![]() 的解析式;
的解析式;
![]() 现将抛物线
现将抛物线![]() 绕着点
绕着点![]() 旋转
旋转![]() 后得到抛物线
后得到抛物线![]() ,若抛物线
,若抛物线![]() 的顶点为
的顶点为![]() ,当
,当![]() ,且顶点
,且顶点![]() 在抛物线
在抛物线![]() 上时,求
上时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
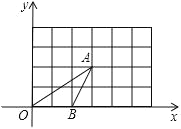
【题目】如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
(1)在图中画出△DEF;
(2)点E是否在直线OA上?为什么?
(3)△OAB与△DEF______位似图形(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
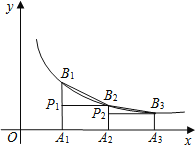
【题目】如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=![]() (x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+Sn=__.
(x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+Sn=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com