
【题目】如图,抛物线![]() 与
与![]() 轴交于A (-1,0),B (5,0)两点,直线
轴交于A (-1,0),B (5,0)两点,直线![]() 与y轴交于点
与y轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是x轴上方的抛物线上一动点,过点
是x轴上方的抛物线上一动点,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
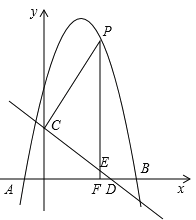
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,是否存在点
的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)y=-x2+4x+5.(2)m=2或m=![]() .(3)(-
.(3)(-![]() ,
,![]() ),(4,5),(3-
),(4,5),(3-![]() ,2
,2![]() -3)
-3)
【解析】
试题分析:(1)利用待定系数法求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程求解;
(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到点P坐标.
试题解析:(1)将点A、B坐标代入抛物线解析式,得:
![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为:y=-x2+4x+5.
(2)∵点P的横坐标为m,
∴P(m,-m2+4m+5),E(m,-![]() m+3),F(m,0)
m+3),F(m,0)
∴PE=|yP-yE|=|(-m2+4m+5)-(-![]() m+3)|=|-m2+
m+3)|=|-m2+![]() m+2|,
m+2|,
EF=|yE-yF|=|(-![]() m+3)-0|=|-
m+3)-0|=|-![]() m+3|.
m+3|.
由题意,PE=5EF,即:|-m2+![]() m+2|=5|-
m+2|=5|-![]() m+3|=|-
m+3|=|-![]() m+15|
m+15|
①若-m2+![]() m+2=-
m+2=-![]() m+15,整理得:2m2-17m+26=0,
m+15,整理得:2m2-17m+26=0,
解得:m=2或m=![]() ;
;
②若-m2+![]() m+2=-(-
m+2=-(-![]() m+15),整理得:m2-m-17=0,
m+15),整理得:m2-m-17=0,
解得:m=![]() 或m=
或m=![]() .
.
由题意,m的取值范围为:-1<m<5,故m=![]() 、m=
、m=![]() 这两个解均舍去.
这两个解均舍去.
∴m=2或m=![]() .
.
(3)假设存在.
作出示意图如下:
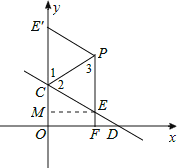
∵点E、E′关于直线PC对称,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y轴,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四边形PECE′是菱形.
当四边形PECE′是菱形存在时,
由直线CD解析式y=-![]() x+3,可得OD=4,OC=3,由勾股定理得CD=5.
x+3,可得OD=4,OC=3,由勾股定理得CD=5.
过点E作EM∥x轴,交y轴于点M,易得△CEM∽△CDO,
∴![]() ,即
,即![]() ,解得CE=
,解得CE=![]() |m|,
|m|,
∴PE=CE=![]() |m|,又由(2)可知:PE=|-m2+
|m|,又由(2)可知:PE=|-m2+![]() m+2|
m+2|
∴|-m2+![]() m+2|=
m+2|=![]() |m|.
|m|.
①若-m2+![]() m+2=
m+2=![]() m,整理得:2m2-7m-4=0,解得m=4或m=-
m,整理得:2m2-7m-4=0,解得m=4或m=-![]() ;
;
②若-m2+![]() m+2=-
m+2=-![]() m,整理得:m2-6m-2=0,解得m1=3+
m,整理得:m2-6m-2=0,解得m1=3+![]() ,m2=3-
,m2=3-![]() .
.
由题意,m的取值范围为:-1<m<5,故m=3+![]() 这个解舍去.
这个解舍去.
当四边形PECE′是菱形这一条件不存在时,
此时P点横坐标为0,E,C,E'三点重合与y轴上,菱形不存在.
综上所述,存在满足条件的点P,可求得点P坐标为(-![]() ,
,![]() ),(4,5),(3-
),(4,5),(3-![]() ,2
,2![]() -3)
-3)


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线![]() 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线![]() 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定:对角线互相垂直的凸四边形叫做“正垂形”.
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“正垂形”的有 ;
②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形 “正垂形”.(填“是”或“不是”)
(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ACB﹣∠CDB=∠ACD﹣∠CBD,当![]() ≤OE≤
≤OE≤![]() 时,求AC2+BD2的取值范围;
时,求AC2+BD2的取值范围;
(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“正垂形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.试直接写出满足下列三个条件的抛物线的解析式;
①![]() ; ②
; ②![]() ; ③“正垂形”ABCD的周长为12
; ③“正垂形”ABCD的周长为12![]() .
.
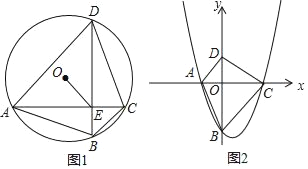
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 单位的速度向点
单位的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 同时出发,以每秒
同时出发,以每秒![]() 单位的速度向点
单位的速度向点![]() 运动,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为
运动,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为![]() 秒.
秒.
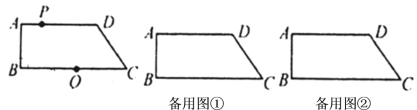
(1)当![]() 时,若以点
时,若以点![]() ,
,![]() 和点
和点![]() ,
,![]() ,
,![]() ,
,![]() 中的两个点为顶点的四边形为平行四边形,且线段
中的两个点为顶点的四边形为平行四边形,且线段![]() 为平行四边形的一边,求
为平行四边形的一边,求![]() 的值.
的值.
(2)若以点![]() ,
,![]() 和点
和点![]() ,
,![]() ,
,![]() ,
,![]() 中的两个点为顶点的四边形为菱形,且线段
中的两个点为顶点的四边形为菱形,且线段![]() 为菱形的一条对角线,请直接写出
为菱形的一条对角线,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与徒步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
(1)求图中的a值.
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C到第二次经过点C,所用时间为1.75小时.
①求AB所在直线的函数解析式;
②请你直接回答,此人走完全程所用的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E,下面判断中:①当△ABC为等边三角形时,△ODE是等边三角形;②当△ODE是等边三角形,△ABC为等边三角形;③当∠A=45°时,△ODE是直角三角形;④当△ODE是直角三角形时,∠A=45°.正确的结论有( )
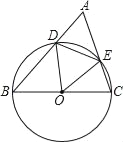
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
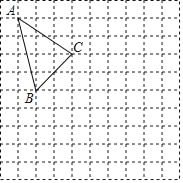
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C的坐标分别为A(﹣3,4)C(0,2)
(1)请在网格所在的平面内建立平面直角坐标系,并写出点B的坐标;
(2)画出△ABC关于原点对称的图形△A1B1C1;
(3)求△ABC的面积;
(4)在x轴上存在一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4
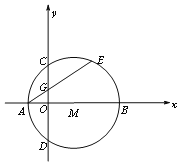
(1)求点C的坐标;
(2)连接MG、BC,求证:MG∥BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com