
【题目】徐老师给爱好学习的小敏和小捷提出这样一个问题:如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
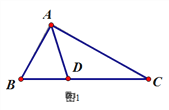
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)请你任意选择一种思路继续完成下一步的证明.
【答案】答案见解析
【解析】试题分析:小敏的方法是利用角平分线添加辅助线,构造全等三角形,△ABD和△AED证明AB+BD=AC.小捷的方法构造等腰三角形AEC,EAD,证明AB+BD=AC.
试题解析:
小敏的证明思路是:如图2,在AC上截取AE=AB,连接DE.(如图2)
∵AD是∠BAC的平分线,
∴∠BAD=∠EAD,
在△ABD和△AED中,
AB=AE,
∠BAD=∠EAD,
AD=AD,
∴△ABD≌△AED(SAS),
∴BD=DE,∠ABD=∠AED,
∵∠AED=∠EDC+∠C,∠B=2∠C,
∴∠EDC=∠C,
∴DE=EC,即AB+BD=AC;
小捷的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.
∴∠E=∠BAE,
∵∠ABC=∠E+∠BAE,
∴∠ABC=2∠E,
∵∠ABC=2∠C,
∴∠E=∠C,
∴△AEC是等腰三角形,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠ADE=∠DAC+∠C,∠DAE=∠BAD+∠BAE,
∴∠ADE=∠DAE,
∴EA=ED=AC,
∴AB+BD=AC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】用四舍五入法对数据6.21496按括号中的要求分别取近似值,其中正确的是( )
A. 6.21(精确到0.01) B. 6.214(精确到百分位)
C. 6.21(精确到十分位) D. 6.2149(精确到0.0001)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,壁虎在一座底面半径为 2 米,高为 5 米的油罐的下底边沿点 A处,它 发现在自己的正上方油罐上边缘的点 B处有一只害虫,便决定捕捉这只害虫,为了不引起害 虫的注意,它故意不走直线,而是绕着油罐,沿一条螺旋路线,从背后对害虫进行突然袭击.结 果,壁虎偷袭成功,获得了一顿美餐.请问壁虎至少要爬行多少路程 才能捕到害虫?(π取 3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数.
(2)由(1)小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;②4a﹣2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
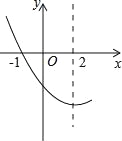
A.①②③ B.②④⑤ C.①③④ D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)中编号①②③④的四个三角形中,关于y轴对称的两个三角形的编号为______;关于x轴对称的两个三角形的编号为______.在图(2)中,画出△ABC关于x轴对称的图形△A1B1C1,并分别写出点A1,B1,C1的坐标.
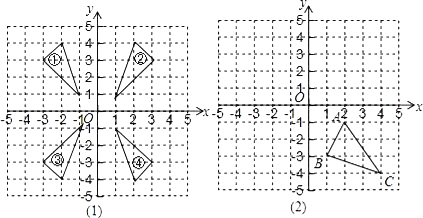
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com