
【题目】问题引入:
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】试题分析:(1)点O是∠ABC和∠ACB平分线的交点,所以∠BOC=180°-∠OBC-∠OCB=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-α)=
(180°-α)=![]() ;同理得图2:∠BOC=
;同理得图2:∠BOC=![]() ;(2)见解析(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,∠A=α,则∠BOC=180°-∠OBC-∠OCB=180°-
;(2)见解析(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,∠A=α,则∠BOC=180°-∠OBC-∠OCB=180°-![]() (∠DBC+∠ECB)=180°-
(∠DBC+∠ECB)=180°-![]() (180°-∠ABC+180°-∠ACB)=180°-
(180°-∠ABC+180°-∠ACB)=180°-![]() (180°+180°-∠ABC-∠ACB)= 180°-
(180°+180°-∠ABC-∠ACB)= 180°-![]() (180°+
(180°+![]() )=
)=![]() .
.
试题解析:
(1)![]() ,
,![]() ;
;
(2)![]() ,
,
理由:∵∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,
∠ECB,∠A=α,
∴∠BOC=180°-![]() (∠DBC+∠ECB)
(∠DBC+∠ECB)
=180°-![]() [360°-(∠ABC+∠ACB)]
[360°-(∠ABC+∠ACB)]
=180°-![]() [360°-(180°-∠A)]
[360°-(180°-∠A)]
=180°-![]() (180°+∠α)
(180°+∠α)
=180°-60°-![]() ∠α
∠α
=120°-![]() ∠α.;
∠α.;
(3)![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
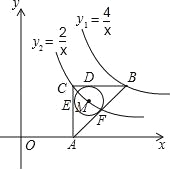
【题目】如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=![]() 的图象经过点B;反比例函数y2=
的图象经过点B;反比例函数y2=![]() 的图象经过点C(
的图象经过点C(![]() ,m).
,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市旅游文化商店自制了一款文化衫,每件成本价为20元,每天销售150件:
(1)若要每天的利润不低于2250元,则销售单价至少为多少元?
(2)为了回馈广大游客,同时也为了提高这种文化衫的认知度,商店决定在“五一”节当天开展促销活动,若销售单价在(1)中的最低销售价的基础上再降低![]() m%,则日销售量可以在150件基础上增加
m%,则日销售量可以在150件基础上增加![]() m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值.
m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐老师给爱好学习的小敏和小捷提出这样一个问题:如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
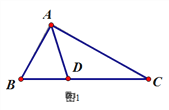
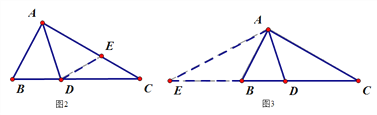
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)请你任意选择一种思路继续完成下一步的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是⊙O外的一点,PB与⊙O相交于点A、B,PD与⊙O相交于C、D,AB=CD.
求证:(1)PO平分∠BPD;
(2)PA=PC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com