
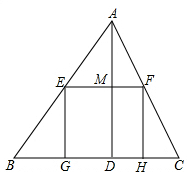
 △ABC是一块锐角三角形材料,边BC=120cm,高AD=80cm,要把它加工成矩形零件EFGH,使矩形的一边GH在BC上,其余两个顶点E、F在AB,AC上,
△ABC是一块锐角三角形材料,边BC=120cm,高AD=80cm,要把它加工成矩形零件EFGH,使矩形的一边GH在BC上,其余两个顶点E、F在AB,AC上,分析 (1)根据EF∥BC,得出△AEF∽△ABC,进而得出EF:BC=AM:AD;
(2)设EF=x,EG=y,利用相似三角形的性质用x表示出y即可;
(3)根据矩形面积公式求出S与x之间的解析式,运用公式求抛物线顶点的横坐标即可.
解答 (1)证明:∵四边形EFHG是矩形,
∴EF∥BC,
∴△AEF∽△ABC,
∴$\frac{AM}{AD}$=$\frac{EF}{BC}$;
(2)解:设EF=x,EG=y,
故$\frac{80-y}{80}$=$\frac{x}{120}$,
解得:y=-$\frac{2}{3}$x+80.
(3)S矩形EFHG=EG•EF=(-$\frac{2}{3}$x+80)•x.
即S=-$\frac{2}{3}$x2+80x.
∴当x=-$\frac{b}{2a}$=60时,矩形EGHF的面积最大.
点评 本题主要考查了相似三角形的应用、矩形EGHF的面积的表达,把问题转化为二次函数,利用二次函数的性质是解决问题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
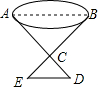 如图,要测量一池塘两端AB的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长至D,使CD=$\frac{1}{5}$CA,连接BC,并延长至E,使CE=$\frac{1}{5}$CB,连接ED,如果量出DE=25m,那么池塘宽AB等于多少?
如图,要测量一池塘两端AB的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长至D,使CD=$\frac{1}{5}$CA,连接BC,并延长至E,使CE=$\frac{1}{5}$CB,连接ED,如果量出DE=25m,那么池塘宽AB等于多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
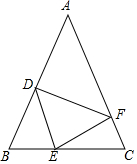 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+3)=x2+3x | B. | 2n2-mn-n=2n(n-m-1) | ||
| C. | -x2-4y2+4xy=-(x-2y)2 | D. | 2x3-8x=2x(x2-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com